Помогите решить неравенство
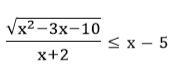
Ответы
ОДЗ:
x∈(-∞; -2) U [5;+∞)
Решаем на каждом из промежутков ОДЗ.
На [5:+∞)
(x+2) >0 ⇒ умножаем обе части неравенства на (х+2).
Знак неравенства при этом не меняется
Замена переменной:
⇒
⇒
или
Обратная замена:
или
x=-2 или x=5 или ⇒
.
x=5 ∈ [5;+∞) или D=9+44=53; или
. c учетом x∈ [5:+∞) и .
а
получаем о т в е т.
На (-∞;- 2)
(x+2) <0 ⇒ умножаем обе части неравенства на (х+2).
Знак неравенства при этом меняется
Та же замена.
⇒
⇒
⇒
c учетом x∈ (-∞; -2) и , так как
;
.
получаем о т в е т.
Объединяем ответы двух рассмотренных случаев:
- О т в е т.