Предмет: Математика,
автор: borisradchenko7699
Помогите решить сложное уравнение
Приложения:
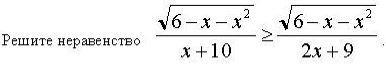
Ответы
Автор ответа:
0
Ответ:
x E [ 1,2 ] U { -3 }
Пошаговое объяснение:
(√(6-x-x^2))/(x+10) ≥ (√6-x-x^2)/(2x+9), x E [ -3,2 ]
(√(6-x-x^2))/(x+10) - (√6-x-x^2)/(2x+9) ≥ 0
((2x+9)√(6-x-x^2)-(x+10)√(6-x-x^2)) / (x+10)(2x+9) ≥ 0
{ (2x+9)√(6-x-x^2)+(-x-10)√(6-x-x^2)) ≥ 0
{ (x+10)(2x+9) > 0
{ (2x+9)√(6-x-x^2)+(-x-10)√(6-x-x^2)) ≥ 0
{ (x+10)(2x+9) < 0
{ x E [ 1, +∞] U {-3}
{ x E [ -∞, -10] U [ -(9/2), +∞]
{ x E [ -∞, 1] U [ 2 ]
{ x E [ -10] U [ -(9/2)]
x E [ -10, -(9/2) ] U [1, +∞] U {-3}, x E [ -3,2 ]
x E [ 1,2 ] U { -3 }
Похожие вопросы
Предмет: Русский язык,
автор: tbegmatov
Предмет: Английский язык,
автор: 989999
Предмет: Русский язык,
автор: MrWaness
Предмет: Алгебра,
автор: ЭHэнни
Предмет: Геометрия,
автор: Hahahah22904