Question

Помогите! (лучше на бумаге):

Answer 1

6.1. Пусть прямая АВ задана уравнением вида $y=bx+c$, где $b$ и $c$ - некоторые числа. Тогда выполняются равенства $3=4b+c$ и $-11=-3b+c$.

Параметры $b$ и $c$ найдем из системы $\left \{ {{4b+c=3} \atop {-3b+c=-11}} \right.$

Вычтем из первого уравнения второе:

$4b+c-(-3b+c)=3-(-11);\\\\4b+c+3b-c=3+11;\\\\7b=14\Rightarrow b=2$

Подставим $b$ в первое уравнение: $4\cdot2+c=3\Rightarrow c=-5$. Искомое уравнение прямой АВ - $y=2x-5$.

Запишем уравнение второй прямой в том же виде: $-3x+2y=7\Rightarrow y=1.5x+3.5.$

Уравнение прямой, параллельной прямой $y=1.5x+3.5.$, имеет вид $y=1.5x+d$, где $d\neq 3.5$ - некоторое число, т.к. угловые коэффициенты параллельных прямых совпадают.

Ординаты точки пересечения прямых $y=1.5x+d$ и $y=2x-5$  равны, поэтому $1.5x+d=2x-5$. При этом, т.к. по условию точка пересечения лежит на оси ОУ, то x = 0. Соответственно, $d = -5$

Уравнение искомой прямой - $y=1.5x-5$.

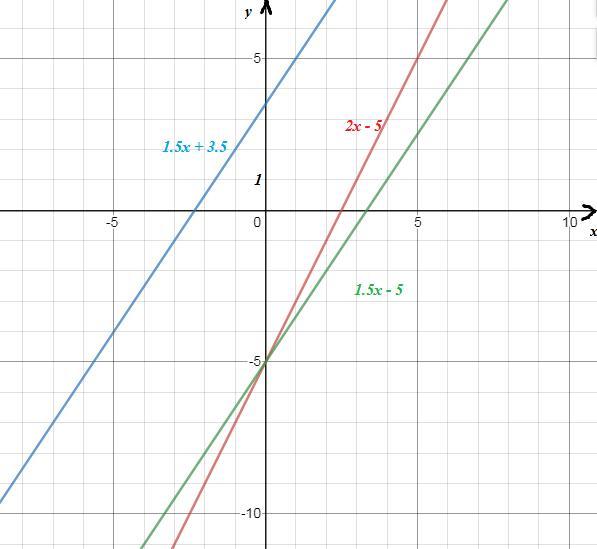
Изображение прямых - приложение 1.

ОТВЕТ: y = 2x - 5;  y = 1,5x - 5.

6.2. Найдем абсциссу точек пересечения прямых:

$-3x+2=2x-8;\\\\2x+3x=2+8;\\\\5x=10\Rightarrow x=2$

Ордината точек пересечения: $y=-3\cdot2+2=-4.$

Точка пересечения прямых - (2; -4).

Если прямая $ax-3y=6a$ проходит через данную точку, то выполняется равенство

$2a-3\cdot(-4)=6a;\\\\12=4a;\Rightarrow a=3$

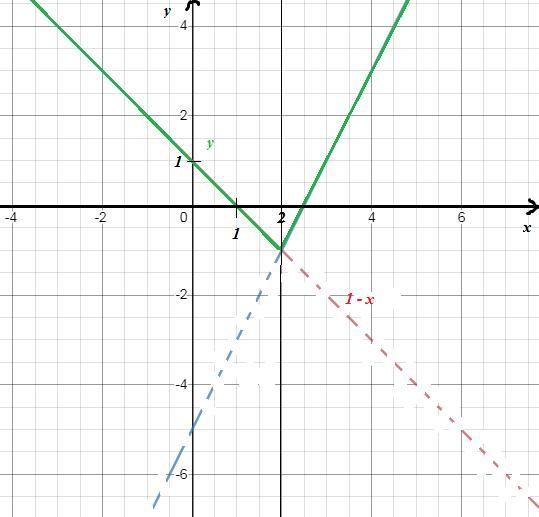
Уравнение данной прямой имеем вид $2x-3y=12\Rightarrow y=\frac{2}{3}x-4$Изображение прямых - приложение 2.

ОТВЕТ: a = 3.

6.3. График функции в 3 приложении.