Предмет: Алгебра,
автор: Аноним
Алгебра 8 повторение пройденного
Приложения:
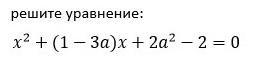
Ответы
Автор ответа:
1
Объяснение:
Ответ: x₁=2a-2 x₂=a+1.
Похожие вопросы
Предмет: Русский язык,
автор: 64743569846
Предмет: Русский язык,
автор: Кармеллита
Предмет: Русский язык,
автор: Багирочкаааа
Предмет: Литература,
автор: существ4
Предмет: Геометрия,
автор: uhjvjvjkybz