Предмет: Алгебра,
автор: iana180305
Решите пожалуйста, даю 20 баллов
Приложения:
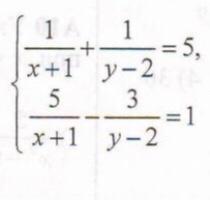
Ответы
Автор ответа:
1
Ответ:
1/(x+1) + 1/(y-2)= 5
5/(x+1)-3/(y-2)=1
У нас есть похожие части, введем новые переменные
1/(х+1) обозначим буквой a
1/(y-2) - буквой b, тогда
⇒
1/(x+1)=2
1=2x+2
2x=-1
x=-0.5
1/(y-2)=3
1=3y-6
3y=7
y=2 1/3
Автор ответа:
0
Ответ:
Похожие вопросы
Предмет: Другие предметы,
автор: luliya01
Предмет: Русский язык,
автор: irichenka2002
Предмет: Другие предметы,
автор: Банан11
Предмет: Физика,
автор: Kirapi
Предмет: Математика,
автор: Руфина157