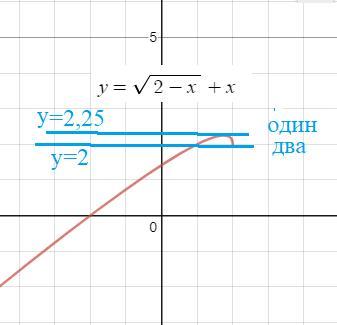Определите, при каких значениях параметра уравнение имеет одно решение √2−х=а−х. Ответ запишите в десятичном виде.
Ответы
ОДЗ:
2-х≥0⇒ х≤2
Возводим в квадрат при условии, что a-x ≥0, т. е x ≤a
2-х=(а-х)²
2-х=а²-2ах+х²
х²-(2а-1)х+а²-2=0
D=(2a-1)²-4(a²-2)=4a²-4a+1-4a²+8=9-4a
Если D=0 ⇒ квадратное уравнение имеет один корень
9-4а=0
а=2,25 уравнение x²-3,5x+(49/16)=0⇒(x-1,75)²=0
x=1,75 - входит в ОДЗ.
x=1,75 - корень уравнения
Если D>0 ⇒ квадратное уравнение имеет два корня
D>0; D=9-4a ⇒9-4a >0 ⇒ a < 2,25
C учетом ОДЗ: x≤2 и условия: x≤a
при 2 ≤а<2,25 уравнение имеет два корня.
Значит, при a ∈(-∞;-2) U {2,25} уравнение имеет один корень
О т в е т. a ∈(-∞;-2) U {2,25}
Графический способ решения.
√(2-x)=a-x
√(2-x)+x=a
Уравнение имеет вид: f(x)=g(x)
f(x)=√(2-x)+x; g(x)=а
Строим график функции y=√(2-x)+x
Область определения x ∈(-∞;2]
y`=0
⇒
⇒
- точка возможного экстремума функции.
Применяем достаточное условие экстремума:
проверяем знак производной при переходе через точку.
При y` >0 функция возрастает
При y` < 0 функция убывает
y_(наиб) = y ( ) =
= 2,25
Прямая y=a пересекает график функции в одной точке
при a ∈ (-∞;2) и при a=2,25
О т в е т. a ∈ (-∞;2) U{2,25}