Предмет: Геометрия, автор: 2759060

две окружности имеют внешнее касание,прямые ab и cd их общие касательные.точки а,в,с,д-точки касания. докажите что в четырехугольник авсд можно вписать окружность.

Ответы

Автор ответа: siestarjoki

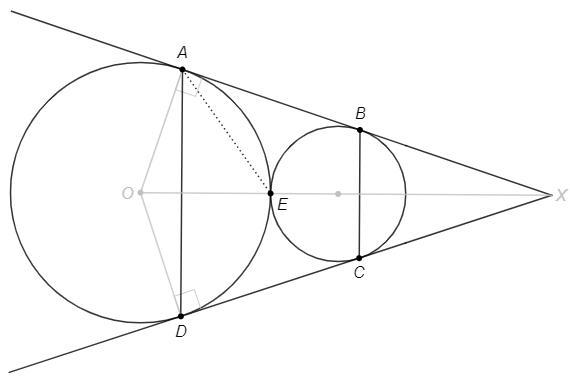
Окружность с центром O вписана в угол X.

△XOA=△XOD по катету и гипотенузе.

XO является биссектрисой углов X и AOD.

Точка касания окружностей E лежит на линии центров (биссектрисе углов X и AOD).

∪AE=∪DE

BAE =∪AE/2 (угол между касательной и хордой) =∪DE/2 =DAE

AE - биссектриса BAD

Аналогично другие углы.

Биссектрисы ABCD пересекаются в точке E.

Следовательно E - центр вписанной окружности ABCD.

Приложения:

Автор ответа: Аноним

Объяснение: см. во вложении

Приложения:

siestarjoki: надо доказать, что O3 лежит на KF. Элементарно, но надо.

siestarjoki: пардон, не надо :)

Предыдущий вопрос

Следующий вопрос

Похожие вопросы

Предмет: Русский язык, автор: lenabunakova8

Днем молчит ночью кричит по лесу летает прохожих пугает

1 год назад

Предмет: Английский язык, автор: katrino4ka08

помогите с переводом пожалуйста!
Organisation and personnel
charts
A business is usually
divided into a number of departments, each being responsible for a specific
range of work (such as production, finance, personnel, marketing). The
structure of the departments and sub-departments can be shown in an
organisation chart. This shows the departments how they are related to each
other, and the lines of communication between them.

Organisation charts
differ from personnel charts. These show the posts held by individuals, their
job titles and, sometimes, the span of control. The charts, therefore, indicate
how responsibilities are divided between different individuals, and who is
responsible to whom.

Despite their
advantages, the charts have three serious limitations.

The amount of work
involved in running a large business is usually too much for the senior managers
to cope with entirely on their own. This means that responsibilities, authority
and duties have to be passed "down the line" to others – i.e. to
middle management and first-line management. This is known as delegation. One
of the arts of management is to know to whom particular tasks can be delegated –
and to whom they should not. Proper delegation means the spreading of the work
load. It also means that particular tasks can be delegated to those who have
special experience or qualifications to deal with them. However, there is
always the risk that the person a task is delegated to will prove to be
incompetent. There is also the risk that unless there is proper "reporting
back", the senior manager will not know what is going on.

Plans are pointless
unless there is a periodic check – a control – on what is being achieved.
Whereas planning is concerned with the future, control is concerned with the
(immediate) past. Problems can arise at any point during the implementation of
a plan. Furthermore, unless a specific check is made on them, they can go
unnoticed for so long that they become impossible to remedy. The controls
should therefore be carefully planned so that they spot-light the problems
which are likely to arise. Also, they should take place regularly.

There
are several different types of control. Some can be measured in

specific "quantity" terms. With these, an actual figure proposed in the
plan

(often known as the budgeted or standard figure) can be compared
with the

figure actually achieved. For example, the planned quantity of raw material

expected to be used, together with its anticipated cost, can be compared

with the actual quantity used and the actual cost. Similarly, the
"standard"

(i.e. anticipated) wage rates and the time a job is expected to take can be

compared with the actual.

1 год назад

Предмет: Другие предметы, автор: Аидоочка07

er besuchen oft die klasse 5 a переведите это на немецком

1 год назад

Предмет: Биология, автор: DariaFkK

Серое вещество мозга образовано...
а) дендритами
б) телами нейронов
в) аксонами
г) дендритами и телами нейронов

8 лет назад

Предмет: Литература, автор: HAL523

Сочините стих про Динару пж очень надо

8 лет назад