Предмет: Геометрия,
автор: malika240318
Дан равнобедренный треугольник ABC. AB
= BC. Высота BK разделена точкой O в
отношении 4:1, считая от вершины.
Найдите, в каком отношении луч AО
делит сторону BC.
malika240318:
Ответьте пожалуйста
Добавил третий способ ( без имён )
спасибо)
Ответы
Автор ответа:
1
Воспользуемся теоремой Ван-Обеля с применением чевиан.
Для этого проведём второй луч ВО.
Отрезки на боковых сторонах обозначим х и у (они равны).
4/1 = (х/у) + (х/у),
4у = 2х или 2у = х.
То есть, боковая сторона ВС разделится лучом АО в отношении 2:1.
Ответ: 2:1.
Приложения:

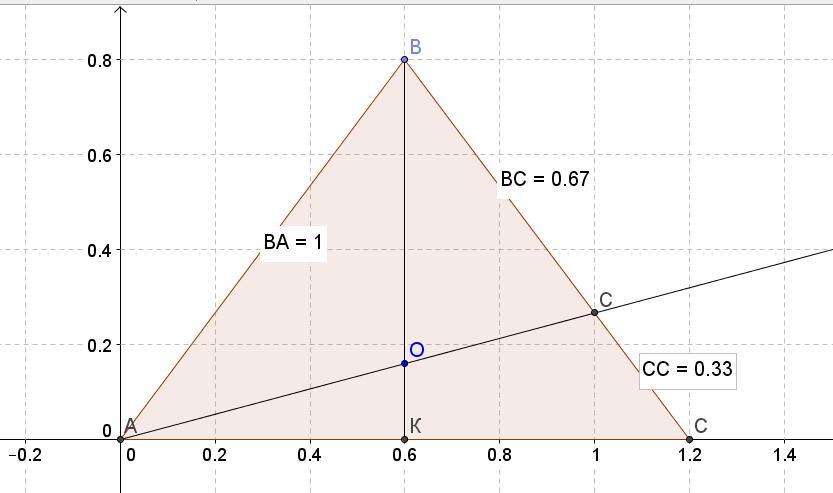
может второй луч будет CO?
Да, верно - луч СО.
ааа, Спасибо большое)
Автор ответа:
2
Ответ:
2 : 1 , ещё 2 способа решения - 1) по теореме Фалеса , 2) по теореме Менелая ( а вдруг вам Ван - Обель не понравился ? )
Объяснение:
Приложения:

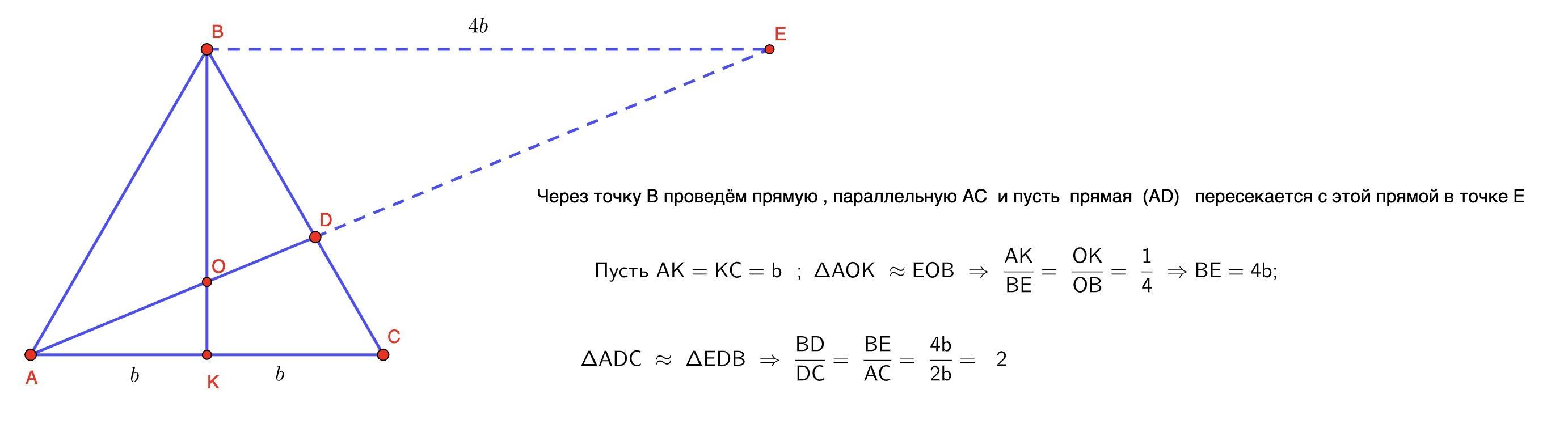
по теореме Менелая, там почему СА/АК =2?
К - середина АС , СА в 2 раза больше АК
ааа, понятно
Похожие вопросы
Предмет: Английский язык,
автор: lobodenko20034
Предмет: Другие предметы,
автор: sruzkova
Предмет: Русский язык,
автор: Angela0505
Предмет: Математика,
автор: chebotarkamill
Предмет: Математика,
автор: оксана669