Question

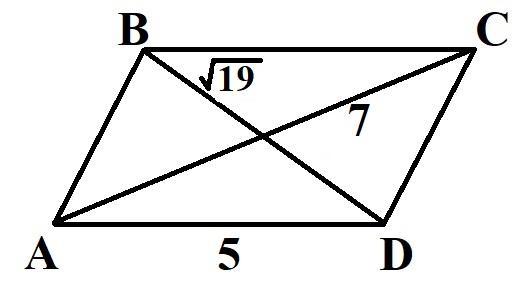
Длины диагоналей параллелограма равны 7 и (корень из 19), а длина одной из сторон равна 5. Найдите периметр параллелограма

Answer 1

Р = 2а + √(2(d1)^2 + 2(d2)^2 - 4a^2)
P = 2•5 + √(2 • 7^2 + 2 • (√19)^2 - 4 • 5^2) =
= 10 + √(98 + 38 - 100) =
= 10 + √36 = 10 + 6 = 16
Ответ: 16

Answer 2

Ответ:

$16$

Пошаговое объяснение:

Дано:

$ABCD-$параллелограмм

$AC=7$

$BD=\sqrt{19}$

$AD=5$

$P_{ABCD}-?$

Решение:

по свойству диагоналей параллелограмма: сумма квадратов длин диагоналей равна сумме квадратов длин всех его сторон

$AC^2+BD^2=AB^2+BC^2+CD^2+AD^2$

Так как в параллелограмме $CD=AB,~~BC=AD$ , то

$AC^2+BD^2=2(AB^2+AD^2) \\ \\ AB^2+AD^2=\frac{AC^2+BD^2}{2} \\ \\ AB^2=\frac{AC^2+BD^2}{2}-AD^2=\frac{7^2+(\sqrt{19})^2}{2}-5^2=\frac{49+19}{2}-25=\frac{68}{2}-25=\\ \\=34-25=9$

Так как $AB>0$, то $AB=\sqrt{9}=3$

$P_{ABCD}=AB+BC+CD+AD=2(AB+AD)=2\cdot(3+5)=2\cdot 8 =16$