Предмет: Геометрия,
автор: ifyounoob
Дана трапеция ABCD с основаниями AD и BC. Известно, что AB = BD. Пусть точка M - середина боковой стороны CD , а O - точка пересечения отрезков AC и BM . Докажите, что треугольник BOC - равнобедренный.
Ответы
Автор ответа:
2
Решение : /////////////////////////////////
Приложения:

Автор ответа:
2
Дана трапеция ABCD с основаниями AD и BC. Известно, что AB = BD. Пусть точка M - середина боковой стороны CD , а O - точка пересечения отрезков AC и BM . Докажите, что треугольник BOC - равнобедренный.
Объяснение:
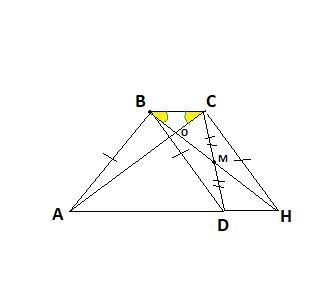
Пусть СH║BD ⇒ DВСH-параллелограмм ( по определению параллелограмма) . СH=BD=AB ⇒ABCH - равнобедренная трапеция ⇒АС=ВН.
ΔАВС=ΔНСВ по 3-м сторонам АС=ВН,АВ=СН, ВС-общая ⇒ соответственные элементы равны ∠ВСО=∠ОВС ⇒треугольник BOC - равнобедренный по признаку равнобедренного треугольника
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Yeseniya545
Предмет: Қазақ тiлi,
автор: RafaiLka
Предмет: Русский язык,
автор: dibil1231
Предмет: Биология,
автор: умник1362
Предмет: Алгебра,
автор: JULIA200202