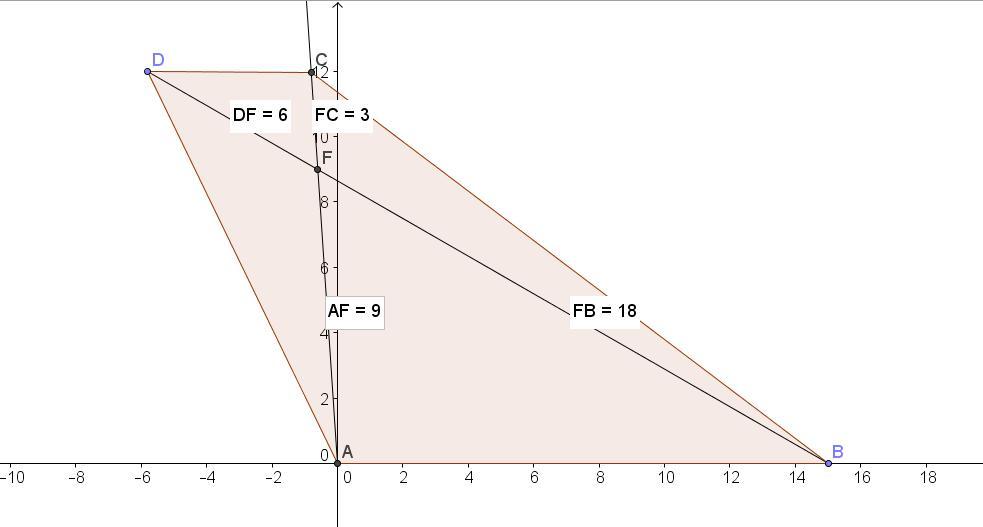
Одна из диагоналей трапеции равна 24 см и делит другую диагональ на отрезки длиной 3 см и 9 см. Большее основание трапеции равно 15 см. Найдите отрезки, на которые точка пересечения диагоналей делит первую диагональ.
Ответы
Ответ:
6см, 18см
Объяснение:
обозначим вершины трапеции А В С Д, диагонали: ВД=24см, и АС и точку их пересечения О.
Диагонали трапеции, пересекаясь делятся между собой в одинаковых пропорциях, а также образуют 2 подобных треугольника ВОС и АОД, стороны которых также имеют такие же пропорции. Если диагональ АС делится точкой на отрезки 3 и 9см, то они имеют пропорции: 3/9=1/3.
В таком же соотношении делится на отрезки ВО и ОД диагональ ВД. Пусть ВО= х, а ДО=3х, составим уравнение:
х+3х=24
4х=24
х=24÷4
х=6
Итак: ВО=6см, тогда ДО=6×3=18см
PS: Не знаю для чего дали данные большего основания, но если нужно найти меньшее основание, то основания также будут иметь пропорции 1/3, и если большее АД=15см, то меньшее ВС=15/3=5см

Пропорция между сторонами треугольников, куда входят диагонали длиной 24 и 12 см равна 2.
Поэтому диагональ в 24 см разделится на отрезки 3*2 = 6 см и 9*2 = 18 см.