Предмет: Алгебра,
автор: Cate213
Вычислить tg2x , где X--- корень уравнения
2log3 (2sinx) — 7logy (2sinx) + 3 = 0
Ответ должен получится- 0,07
Приложения:
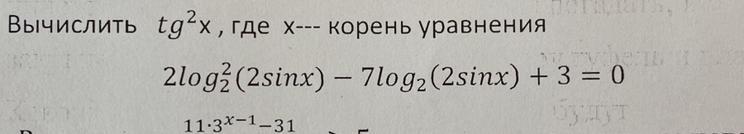
Cate213:
0,07 без минуса
там никак не может быть такой ответ
Ответы
Автор ответа:
1
Ответ:
1
Объяснение:
Замена
Обратная замена:
Автор ответа:
1
Ответ 1.
Решение.
Сам корень находить нет необходимости. Чтобы определить tg^2(x) достаточно вычислить sinx.
Приложения:

Похожие вопросы
Предмет: Русский язык,
автор: kuzolga1
Предмет: Русский язык,
автор: salmovayana
Предмет: Русский язык,
автор: Sima2005
Предмет: Физика,
автор: BlooDkr4