Question

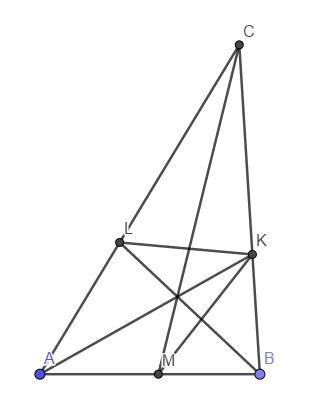
В треугольнике abc со сторонами AB=4 BC=6 AC=7 проведены биссектрисы AK BL CM. НАЙДИТЕ ПЛОЩАДИ ТРЕУГОЛЬНИКА BKM к площади треугольника СKL

Answer 1

Найдём площадь треугольника по формуле Герона

$p=\dfrac{a+b+c}{2}=\dfrac{4+6+7}{2}=8{,}5$

$S=\sqrt{p(p-a)(p-b)(p-c)}=\sqrt{8{,}5(8{,}5-4)(8{,}5-6)(8{,}5-7)}=\dfrac{3}{4}\sqrt{255}$

По свойству биссектрисы мы имеем

$\dfrac{CK}{KB}=\dfrac{AC}{AB}=\dfrac{7}{4};\\ \\ \dfrac{AL}{CL}=\dfrac{AB}{BC}=\dfrac{4}{6}=\dfrac{2}{3};\\ \\ \dfrac{LO}{OK}=\dfrac{CL}{CK}=\dfrac{7}{6}$

Определим отношение площадей треугольника АВС на CKL

$\dfrac{S_{ABC}}{S_{CKL}}=\dfrac{AC\cdot BC\sin C}{CL\cdot CK\sin C}=\dfrac{5x\cdot 11y}{3x\cdot 7y}=\dfrac{55}{21}~~\Rightarrow~~ S_{CKL}=\dfrac{21S_{ABC}}{55}=\dfrac{63\sqrt{255}}{220}$

Аналогично, определим отношение площадей треуг. ABC на BKM

$\dfrac{S_{ABC}}{S_{BKM}}=\dfrac{AB\cdot BC\sin B}{MB\cdot BK\sin B}=\dfrac{13z\cdot11y}{6z\cdot4y}=\dfrac{143}{24}~\Rightarrow~ S_{BKM}=\dfrac{18\sqrt{255}}{143}$

Окончательно имеем $\dfrac{S_{BKM}}{S_{CKL}}=\dfrac{18\sqrt{255}/143}{63\sqrt{255}/220}=\dfrac{40}{91}$.

Ответ: 40 : 91.