17) Дана правильная треугольная пирамида со стороной основания 12. Боковое ребро пирамиды наклонено к плоскости основания под углом в 30о. Найдите объем описанного около пирамиды конуса.
Ответы
Ответ:
V=64π кубических единиц объем искомого конуса.
Пошаговое объяснение:
Рисунок смотрите в приложении.
Объем конуса вычисляется по формуле
(*).
Здесь R - радиус основания конуса, Н - высота конуса.
Найдем радиус основания конуса. Он равен радиусу описанной окружности основания пирамиды.
SO - высота конуса. Точка О - центр вписанной и описанной окружности правильного треугольника.
АО=R - длина радиуса описанной окружности.
Радиус описанной окружности вычисляется по формуле
, где а - это длина стороны треугольника.
единиц.
Из ΔАОS, который по построению прямоугольный (∠О=90°), по условию задачи ∠SAO=30°. Так как это и есть угол между ребром и основанием пирамиды. Теперь из этого треугольника можно найти SO. SO=AO*tg∠SAO. SO=AO*tg30°,
,
SO=4 единицы.
Подставим в формулу (*).
,
V=π*4³ кубических единиц.
V=64π кубических единиц.
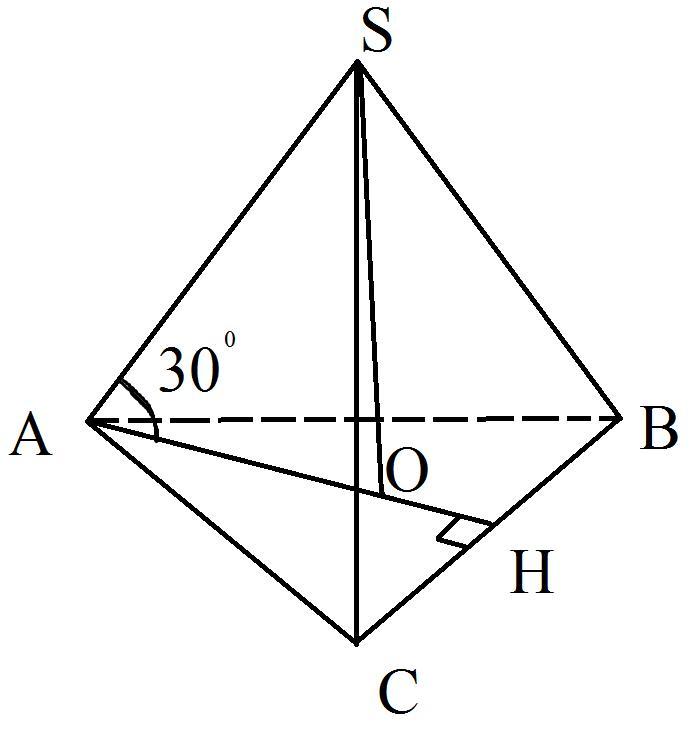
Пошаговое объяснение: см. во вложении
