Предмет: Математика,
автор: Lol081101
Вычислить несобственный интеграл
Приложения:
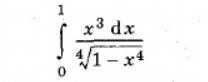
Ответы
Автор ответа:
0
Ответ:
Пошаговое объяснение:
Сначала вычислим неопределённый интеграл.
Пусть 1-x⁴=u ⇒ du=d(1-x⁴)=-4*x³dx x³dx=-du/4. ⇒
Подставляем пределы интегрирования:
Похожие вопросы
Предмет: Українська мова,
автор: vksfgds
Предмет: Русский язык,
автор: avgustinovich
Предмет: Другие предметы,
автор: pasha200090
Предмет: Геометрия,
автор: Аноним
Предмет: Алгебра,
автор: sh0ckerz77141