Предмет: Математика,
автор: Lol081101
Вычислить площадь фигуры ограниченной линиями
Приложения:
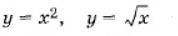
Ответы
Автор ответа:
0
Пошаговое объяснение:
Ответ: S=1/3=0,3333 кв.ед.
Похожие вопросы
Предмет: Українська мова,
автор: vksfgds
Предмет: Русский язык,
автор: avgustinovich
Предмет: Другие предметы,
автор: pasha200090
Предмет: Геометрия,
автор: Аноним
Предмет: Алгебра,
автор: sh0ckerz77141