Предмет: Алгебра,
автор: Аноним
Пожалуйста очень срочно! РЕШИТЕ СПОСОБОМ ГРУППИРОВКИ! РЕШИТЕ ЗАДАЧИ:Б;В;Г.
Приложения:
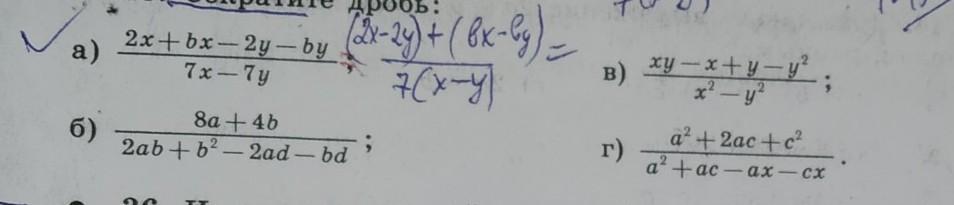
Ответы
Автор ответа:
1
б)
в)
г)
Автор ответа:
0
Ответ:
Похожие вопросы
Предмет: Русский язык,
автор: aynurarzaeva
Предмет: Русский язык,
автор: anutakow
Предмет: Английский язык,
автор: патогенез
Предмет: Физика,
автор: moafine