Предмет: Алгебра,
автор: Nikysk11
Вместо n надо подставить 8
Приложения:
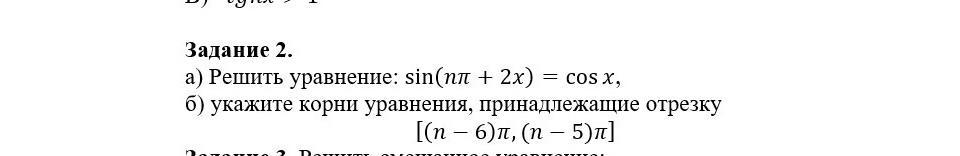
Ответы
Автор ответа:
0
Ответ:
a)
б)
;
;
;
Объяснение:
a)
sin (8π + 2x) = cos x
sin 2x = cos x
2 sin x · cos x - cos x = 0
cos x (2sin x - 1) = 0
1) cos x = 0
2) 2sin x - 1 = 0
sin x = 1/2
б) х∈ [2π; 3π]
1)
k = 2
2)
m = 1
3)
n = 1
Похожие вопросы
Предмет: Русский язык,
автор: osincevelena
Предмет: Русский язык,
автор: mashamashka9
Предмет: Другие предметы,
автор: luchkova96234
Предмет: Биология,
автор: соня1384
Предмет: Математика,
автор: kristinakristi57