Найдите точку минимума функции y=(1-2x)cosx+2sinx+7
на промежутке (0; п/2)
(скобки круглые, если что)
можно решение без интернета
там не понятно
как искать знаки производной на числовой?
Ответы
Ответ:
x = -1/2
Пошаговое объяснение:
Чтобы найти точки максимума и минимума, находим производную и приравниваем ее к нулю. В нашем случае производная будет равна 0, если 2х - 1 = 0, либо sinx = 0. Корень первого уравнения принадлежит промежутку, а все корни синуса не принадлежат промежутку. У нас получилось единственное решение уравнения: х = -1/2, это и есть точка минимума.
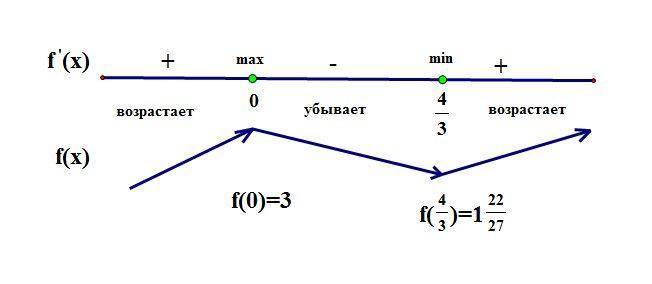
Чтобы найти знаки производной, нужно производную приравнять к нулю и найти все иксы, при которых она равна 0. Дальше их нужно в порядке возрастания выписать на числовую прямую (на второй фотографии это верхняя синяя прямая линия, фотография к данной задаче не относится, она из интернета). Дальше, чтобы определить знаки производной, нужно подставить любой х из промежутка в саму производную. Если производная больше 0, то над промежутком надо написать знак "+", если меньше 0, то "-".
Теперь, зная знаки производной, можно определить промежутки возрастания и убывания функции, точки максимума и минимума. Если производная больше 0, то функция возрастает. Если меньше 0, то убывает. Поэтому под промежутками с плюсом рисуем стрелку вверх, а под промежутками с минусом - вниз (стрелка вверх - функция возрастает, стрелка вниз - убывает).
Теперь там, где стрелки образуют "горку", - точка максимума (на фото это точка 0), а там, где получилась "яма" - точка минимума (на фото это точка 4/3).
Точек максимума и минимума может быть несколько.