Предмет: Математика,
автор: garnerrei
Прошу помогите пожалуйста срочно
С решением
17. Найти скорость движения тела в момент времени t= 2, если закон движения задан формулой s(t) = t (2t+3).
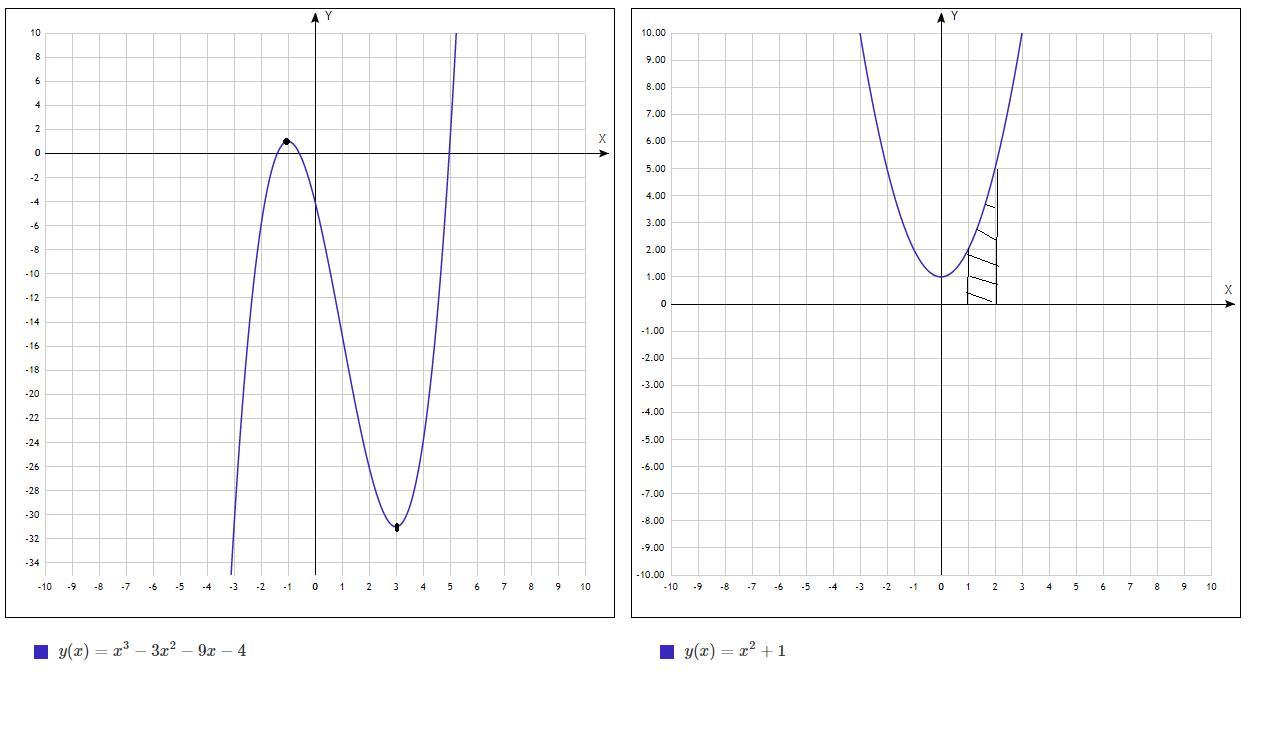
18. Исследовать на экстремум функцию у = х3 – 3х2 -9х - 4. Указать промежутки монотонности функции.
19. Вычислить площадь фигуры, ограниченной линиями у = х2 + 1, у = 0, х = 1, х = 2.
Simba2017:
не ту взяла
S=2t^2+3t; S`=4t+3; S`(2)=V(2)=4*2+3=11
остальные два долго расписывать надо
если можете распишите пожалуйста
а вы что, до сих пор учитесь?
да
хорошо, ждите
спасибо
* * * s(t) =V₀t+at²/2 * * * s(t) = t (2t+3) ⇔ s(t) = 3t+4t²/2 ⇒ V₀ =3 ; a =4 ;
V(t) = V₀+at ; V(2) =3+4*2 = 11 (м/с в системе СИ )
Ответы
Автор ответа:
1
18)функция непрерывна на всем интервале х, нет никаких ограничений, поэтому через производные найду экстремальные точки, в них y`=0
y`=3x^2-6x-9=0
D=36+108=12^2
x1=(6-12)/6=-1;x2=3
знаки производной
++++(-1)-----(3)++++
значит при x=(-∞;-1)U(3;+∞) у возрастает и при х=(-1;3)-убывает
19) S=∫(x^2+1)dx=x^3/3+x=
подстановка по х от 1 до 2
=8/3+2-1/3-1=3 1/3
Приложения:
Автор ответа:
0
Как то так! Надеюсь помогла!
Приложения:

Похожие вопросы
Предмет: Русский язык,
автор: КрендельЙА
Предмет: Русский язык,
автор: Lemur95
Предмет: Қазақ тiлi,
автор: REDFRAG
Предмет: География,
автор: nadyadrogaltseva
Предмет: История,
автор: ппппмммм