Предмет: Алгебра,
автор: pbellay
Решите неравенство, пожалуйста: log2x ≤ 2/log2x-1
Ответы
Автор ответа:
1
pbellay:
Учитель проверил - неверно...
Это точно верный ответ?
Не сказали - я вообще думаю что учитель был не прав
Точно не скажу, но вроде разобрала правое выражение. Ну ответы у вас одинаковые так что думаю это обоснованно
Правильный был (0; 1/2] U [2;4)
Точнее [0; 1/2)U(2;4]
Автор ответа:
1
Ну можно было и проще, ну вообще я сделал прям полное решение)))
Приложения:

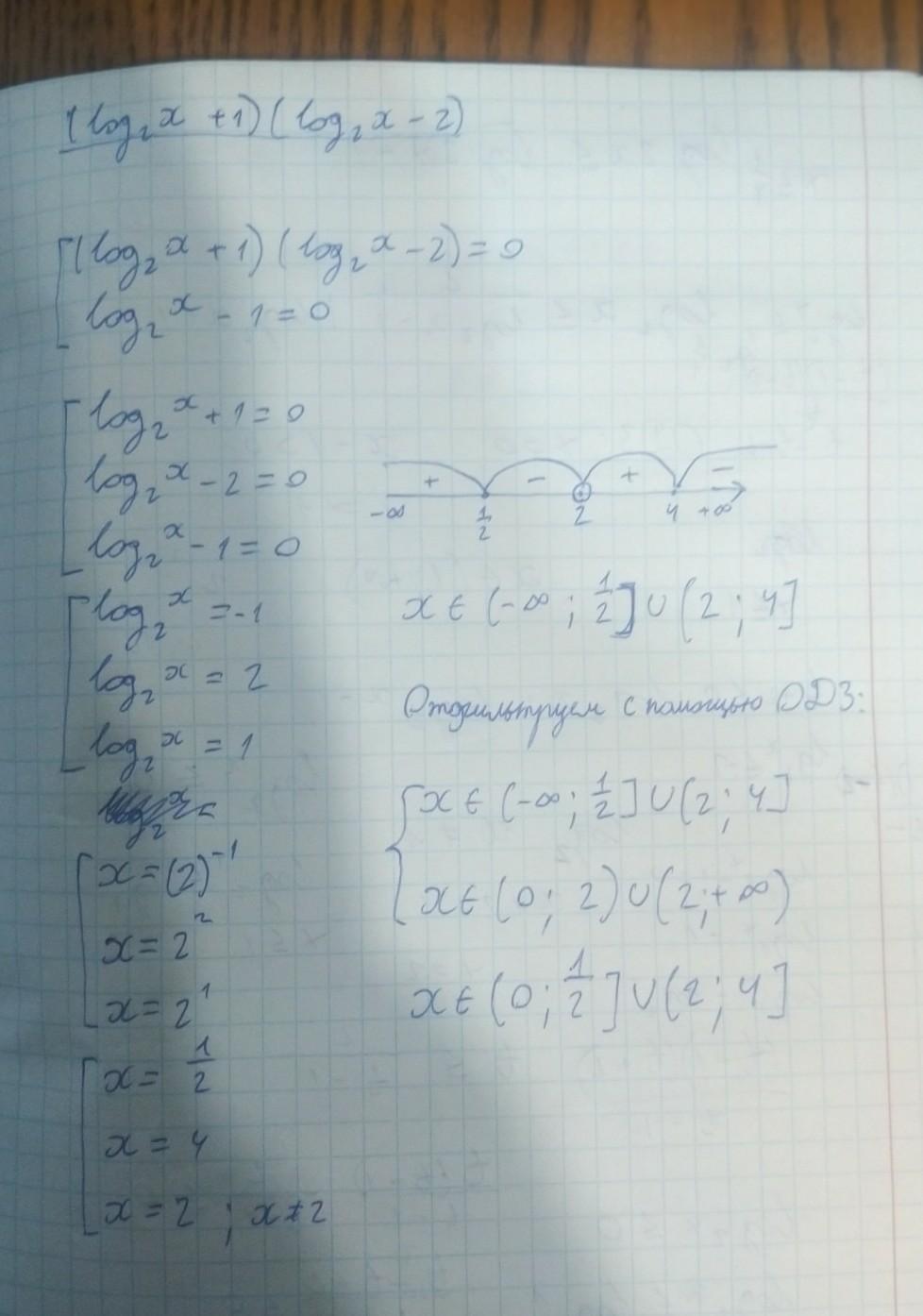
Похожие вопросы
Предмет: Русский язык,
автор: dimagubanov81
Предмет: Русский язык,
автор: rayz37
Предмет: Русский язык,
автор: narjan07
Предмет: Математика,
автор: sla777halk