СРОЧНО НУЖНА ПОМОЩЬ АЛГЕБРА
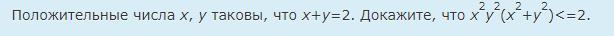
Ответы
Можно решать, конечно, используя производную, но что-то мне подсказывает, что это задача ближе к олимпиадной и до 10 класса.
Итак, есть неравенство, которое надо доказать:
При этом известно, что
Попробуем немного преобразовать выражение
Учитывая, что
Тогда получаем
Сделаем замену
Теперь получаем следующее неравенство
Но важно проанализировать возможные значения
Очевидно, что снизу ограничено нулем, так как произведение положительных чисел положительно, а вот сверху - надо выяснить, но
- парабола с ветвями направленными вниз, то есть её максимум будет в вершине. Формула вершины
То есть
Теперь вернемся к неравенству (2)
Нужно доказать, что оно выполняется. Предположим, что оно выполняется для всех допустимых , соответственно, для
Вычислим, для каких в целом неравенство выполняется. Если найдется хотя бы один промежуток для t внутри (3), в котором неравенство не выполняется, то тогда противоречие и исходное неравенство неверно. Иначе исходное неравенство верно (к чему, по идее, мы и должны прийти).
Решаем (2):
Хоть это кубическое неравенство, но оно совсем несложное. Чтобы решить неравенство методом интервалов, необходимо найти корни уравнения , так как сумма коэффициентов уравнения равна 0, то
- корень, зная это, разложим на множители:
Квадратное уравнение решим стандартно:
Необходимо определить расположение чисел на оси (эти два корня и 1).
Значит, корень с минусом точно меньше 1, раз меньше 0.
А второй корень (с +) сравним с 2, если больше, то тогда этот корень больше 1.
, этого уже достаточно, то есть корни располагаются так:
с "-", 1, с "+". В разложении все коэффициенты положительны, а значит, в самом правом промежутке +, а дальше знаки чередуются, так как нет корней четной кратности.
- + - +
Самое последнее неравенство, от которого мы отталкивались - (4), а значит, нужные нам промежутки с "+", то есть
Первый промежуток включает в себя и , а это значит, что для промежутка (3) неравенство выполняется так же, то есть и исходное неравенство (1) выполняется для всех
, что и требовалось доказать.