Предмет: Математика,
автор: kovalev20031
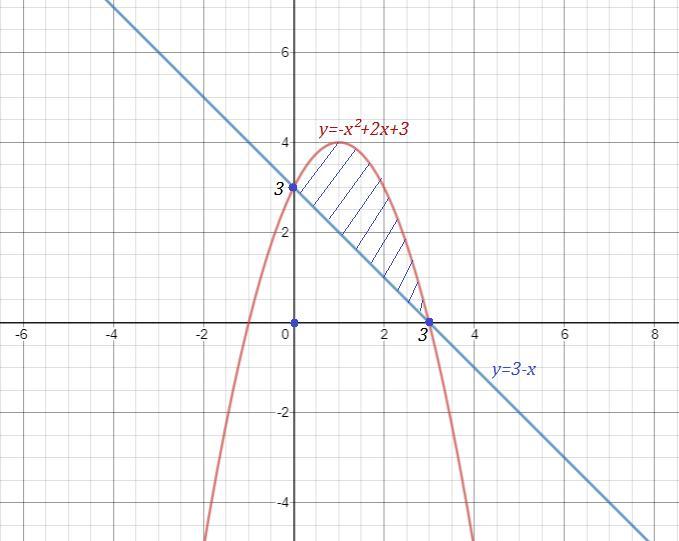
Вычислите площадь фигуры, ограниченными графиками функций:
y = -x² + 2x +3, y = 3 - x
Ответы
Автор ответа:
1
Найдем пределы интегрирования, решив уравнение -х²+2х+3=3-х
х²-3х=0, По Виету х=0, х=3
Найдем определенный интеграл от функции -х²+2х+3-3+х=-х²+3х
Во (-х³/3)+3х²/2 подставим пределы интегрирования и посчитаем площадь. получим(-9+3*9/2)-0=-9+27/2=(27-18)/2=9/2=4.5/ед.кв./
Автор ответа:
1
Ответ:
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: rbarsukova
Предмет: Русский язык,
автор: sabinasabina05
Предмет: Русский язык,
автор: robaltynguzin
Предмет: Математика,
автор: leron0575