Предмет: Алгебра,
автор: didi8888
Корни уравнения x2-5x..... также корни уравнение x3.....Найдите p+q
Приложения:
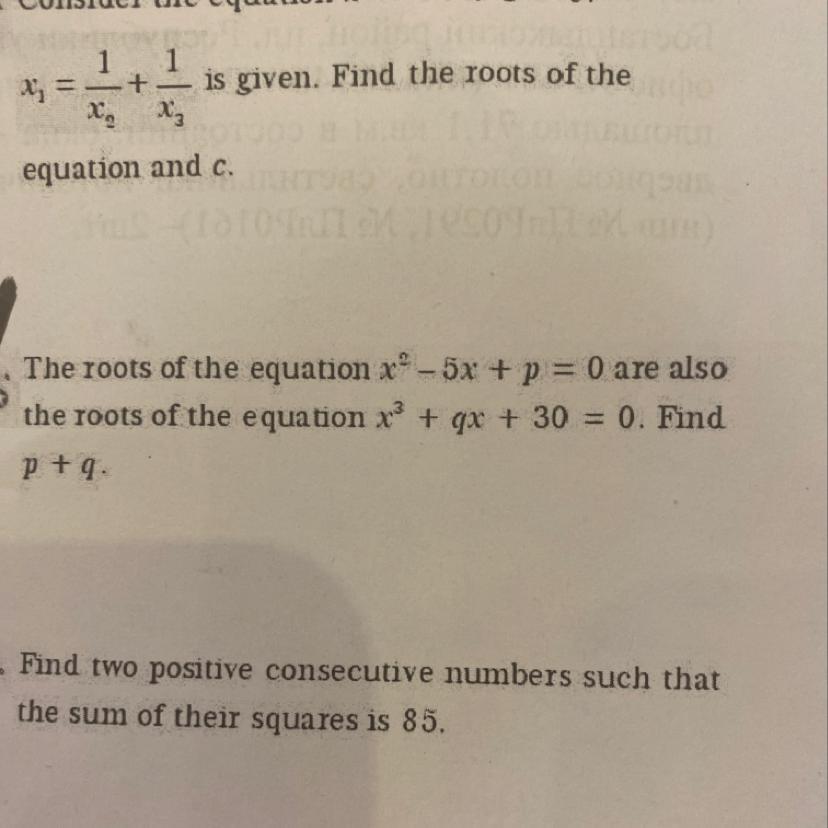
Ответы
Автор ответа:
1
Ответ:
-13
Объяснение:
Рассмотрим уравнение . Пусть
- его корни. По теореме Виета:
Представим кубический многочлен в виде:
Многочлены тождественно равны, если равны коэффициенты при соответствующих степенях. Тогда, имеем:
С учетом условий на имеем:
Тогда квадратное уравнение имеет вид Его корни
. Подставим все три корня в условие на q:
Похожие вопросы
Предмет: Русский язык,
автор: karybekova07
Предмет: Русский язык,
автор: nleshik
Предмет: Русский язык,
автор: Аноним
Предмет: Алгебра,
автор: ПолиночкаПолина