Предмет: Алгебра,
автор: Аноним
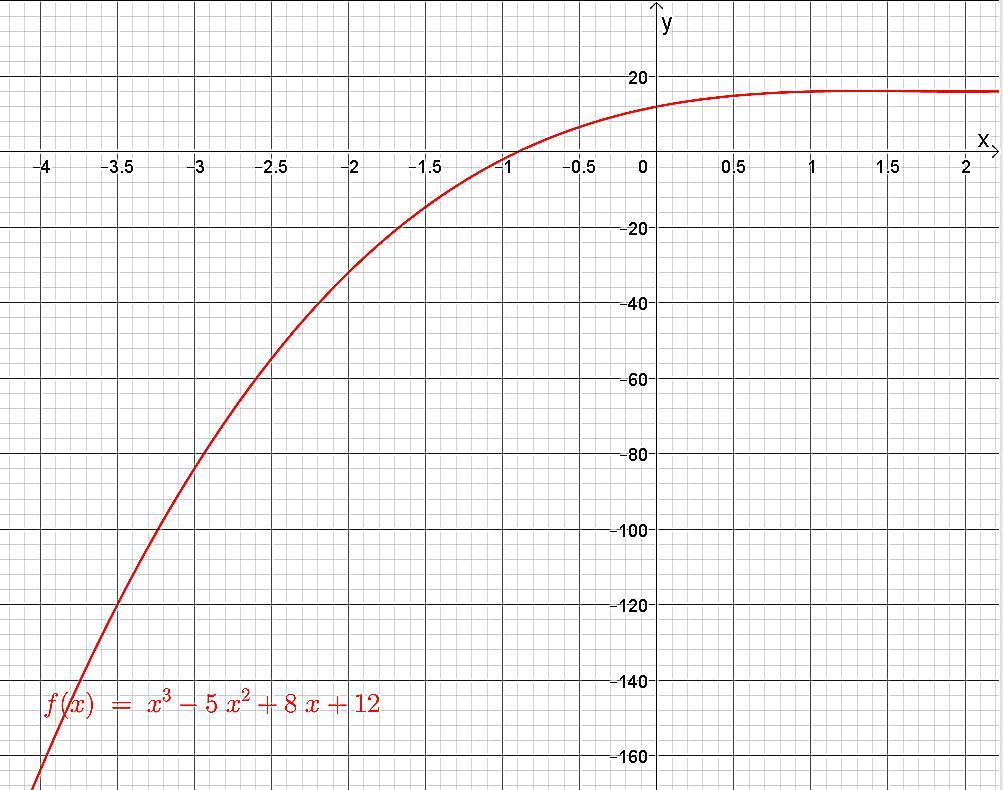
ПОМОГИТЕ ПЖ СРОЧНО РЕШИТЬ.Найдите наименьшее значение функции у=х^3-5х^2+8х+12 на отрезке [-4;1].
Ответы
Автор ответа:
0
Ответ: ymin=y(-4)=-164
Объяснение:
Найдите наименьшее значение функции у = х³ - 5х² + 8х + 12 на отрезке [-4;1].
Найдем значение функции на границах отрезка
у(-4) = (-4)³ - 5·(-4)² +8·(-4) + 12 = -64 - 80 - 32 + 12 = -164
у(1) = 1³ - 5·1² +8·1 + 12 = 1 - 5 + 8 + 12 = 16
Найдем производную функции
у' =(х³ - 5х² + 8х + 12)' = (х³)' - (5х²)' + (8х)' + (12)' = 3x² - 10x +8
Найдем критические точки приравняв производную к нулю
3x² - 10x + 8 = 0
D = (-10)² - 4·3·8 = 100 - 96 = 4
x₁ = (10-2)/(2·3) = 8/6 = 4/3 ≈ 1,33
x₂ = (10+2)/(2·3) = 12/6 = 2
Найденные точки не входят в данный отрезок поэтому значения функции в них находить не будем.
Функция на отрезке монотонна и возрастает. Минимальное значение функции находится в точке x = -4 y(-4) = -164
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: easaturova
Предмет: Русский язык,
автор: ася992
Предмет: Русский язык,
автор: mrlazar1981
Предмет: География,
автор: марипат1