Предмет: Математика,
автор: vladdyachenko1
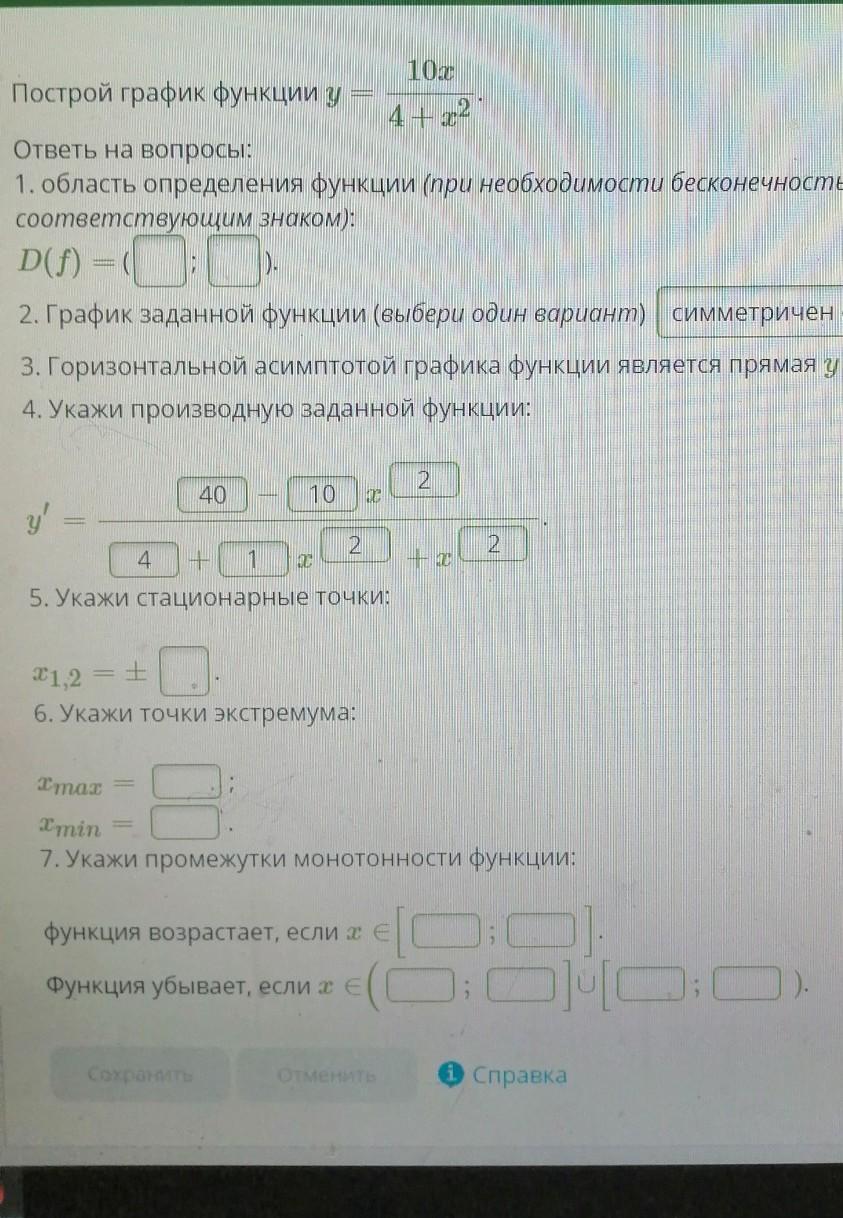
СРОЧНО ПОЖАЛУЙСТА!! нужна ваша помощь.
Приложения:
Ответы
Автор ответа:
1
Ответ:
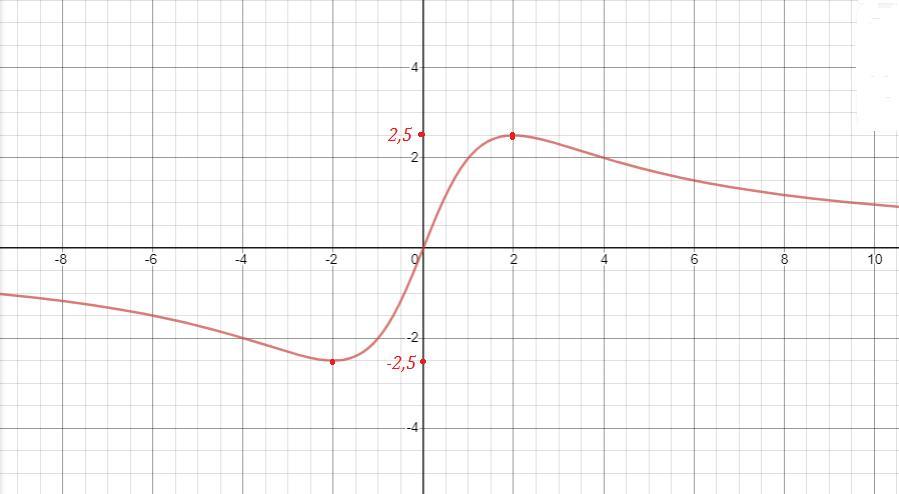
2) График функции симметричен относительно начала координат , точки(0,0)
3) Горизонтальной асимптотой является прямая у=0
7) y(x) возрастает , если
y(x) убывает, если
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: kisa020202
Предмет: Українська мова,
автор: vanyaprosto
Предмет: Русский язык,
автор: Kamilla35
Предмет: История,
автор: vasinhome0212
Предмет: Математика,
автор: рдагнлцн