Бокавая грань четырехугольной пирамиды наклонила к площади основы пол углом 60 градусов. Определите объем этой пирамиды,если радиус вписанного а нее шара равен 3 см.
Ответы
Всё расписано на фото. В случае неуверенности в моём ответе, прошу сообщить об этом:
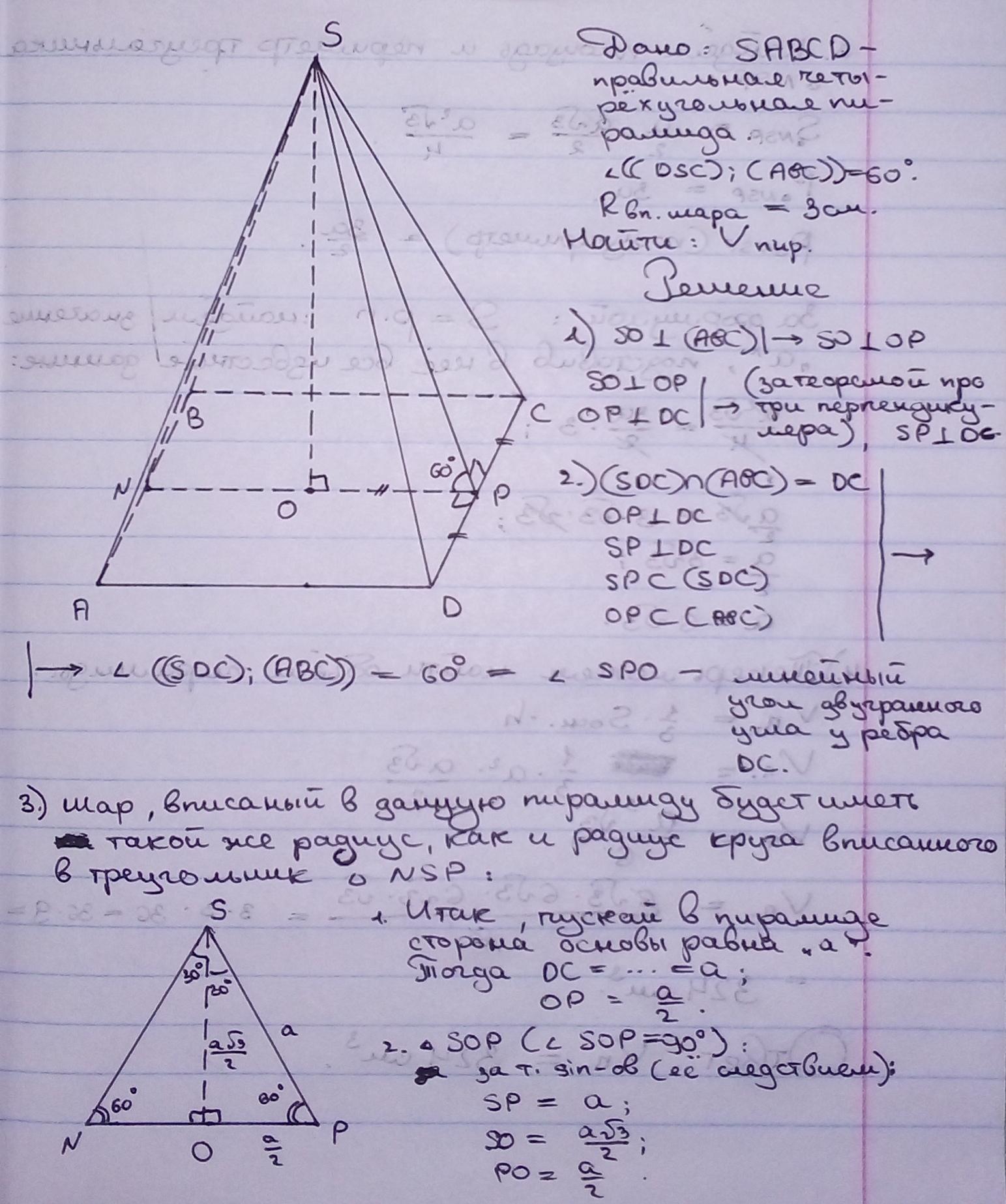

Дано:
В правильную четырёхугольную пирамиду вписан шар.
R шара (ОО1, О1К) = 3 см.
∠SFO = 60˚.
Найти:
V пирамиды - ?
Решение:
Проведём биссектрису О1F.
△O1OF - прямоугольный, так как SO - высота.
=> ∠O1FO = O1FK = 60˚/2 = 30˚
"Если угол прямоугольного треугольника равен 30°, то напротив лежащий катет равен половине гипотенузы".
=> O1F = 3 * 2 = 6 см
Найдём катет OF, по теореме Пифагора: (с = √(a² + b²), где с - гипотенуза; а, b - катеты)
b = √(c² - a²) = √(6² - 3²) = √(36 - 9) = √27 = 3√3 см
Итак, OF = 3√3 см
△SOF - прямоугольный, так как SO - высота.
"Если угол прямоугольного треугольника равен 60°, то напротив лежащий катет равен произведению меньшего катера на √3".
=> SO = OF * √3 = 3√3 * 3 = 9 см.
Итак высота пирамиды SO = 9 см.
MO = OF = 3√3 см, так как SО - высота пирамиды.
=> MF = 3√3 * 2 = 6√3 см
Так как данная пирамида - четырёхугольная, правильная => основание этой пирамиды - квадрат.
"Квадрат - геометрическая фигура, у которой все стороны равны".
=> MF = AB = BC = DC = AD = 6√3 см
S квадрата = а², где а - сторона квадрата.
S квадрата = (6√3)² = 108 см²
V пирамиды = 1/3 * S квадрата * SO = 1/3 * 108 * 9 = 324 см³
Ответ: 324 см³
