Предмет: Алгебра,
автор: viki0290
помогите решить неравенство пожалуйста, подробнее
Приложения:
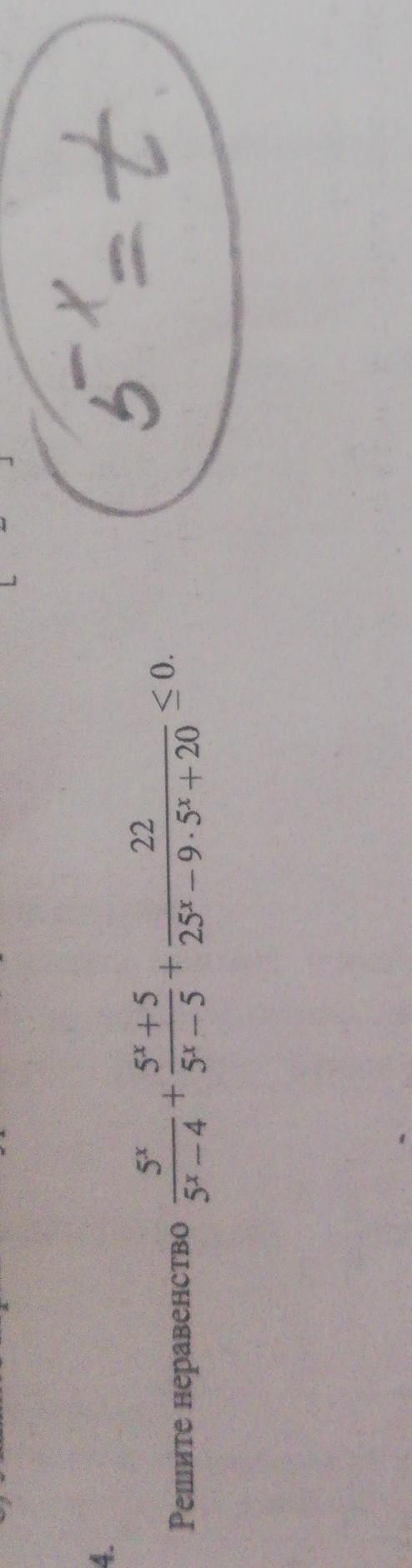
Ответы
Автор ответа:
2
Ответ:
х є {0} U (;1)
Объяснение:
х є {0} U (;1)
Похожие вопросы
Предмет: Українська література,
автор: saidsho
Предмет: Русский язык,
автор: valerij66
Предмет: Русский язык,
автор: karagali
Предмет: Алгебра,
автор: Khkji
Предмет: Математика,
автор: kriptus