Предмет: Математика,
автор: saminullinarsenij
Один из катетов прямоугольного равнобедренного треугольника лежит в плоскости , а другой образует с ней угол 300. Найдите длину гипотенузы, если расстояние от вершины треугольника до плоскости равно 10 см.
saminullinarsenij:
через сколько будет сделана работа
Ответы
Автор ответа:
1
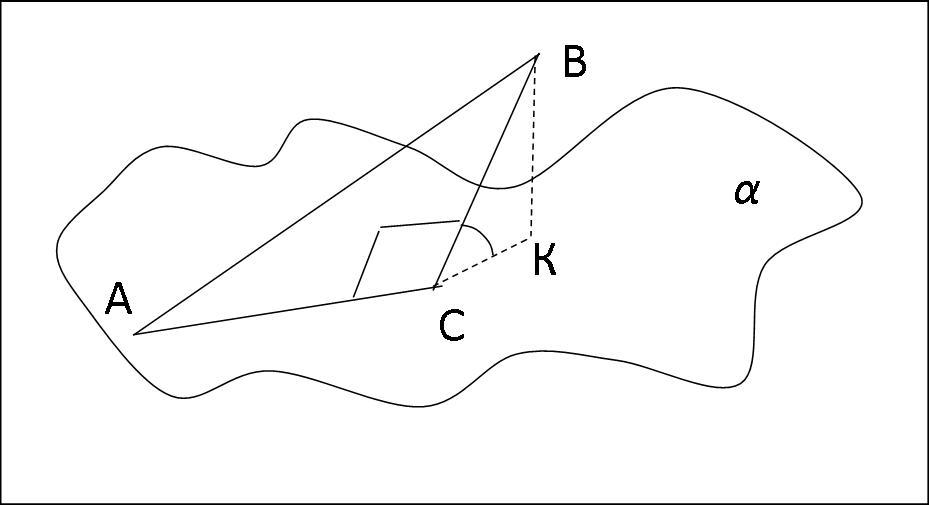
Дано:
ΔАВС;
∠ACB=90°
AC=BC;
α - плоскость
AC ∈ α
BK⊥a
BK = 10см
∠BCK=30°
Найти: АВ
Решение.
1) В прямоугольном ΔВКС катет ВК=10см лежит против угла в 30°, значит, гипотенуза ВС=2ВК
ВС=2 · 10см = 20см
2) В прямоугольном ΔАВС по условию АС=ВС=20см
3) По теореме Пифагора находим гипотенузу АВ.
АВ² = АС² +ВС²
АВ² = 20² + 20²
АВ² = 400 + 400
АВ² = 800
АВ = 20√2 см ≈ 28,3 см
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: MrsHoraaan
Предмет: Қазақ тiлi,
автор: назым1978
Предмет: Русский язык,
автор: smileday
Предмет: Музыка,
автор: eisinykov
Предмет: Математика,
автор: vladislopatin042