Question

СРОЧНО

Вычислить площадь криволинейной трапеции, ограниченной графиком функции

у=х^3–х,

у=0, х=−1, х=2.

Нужно развернутое обьяснение

Answer 1

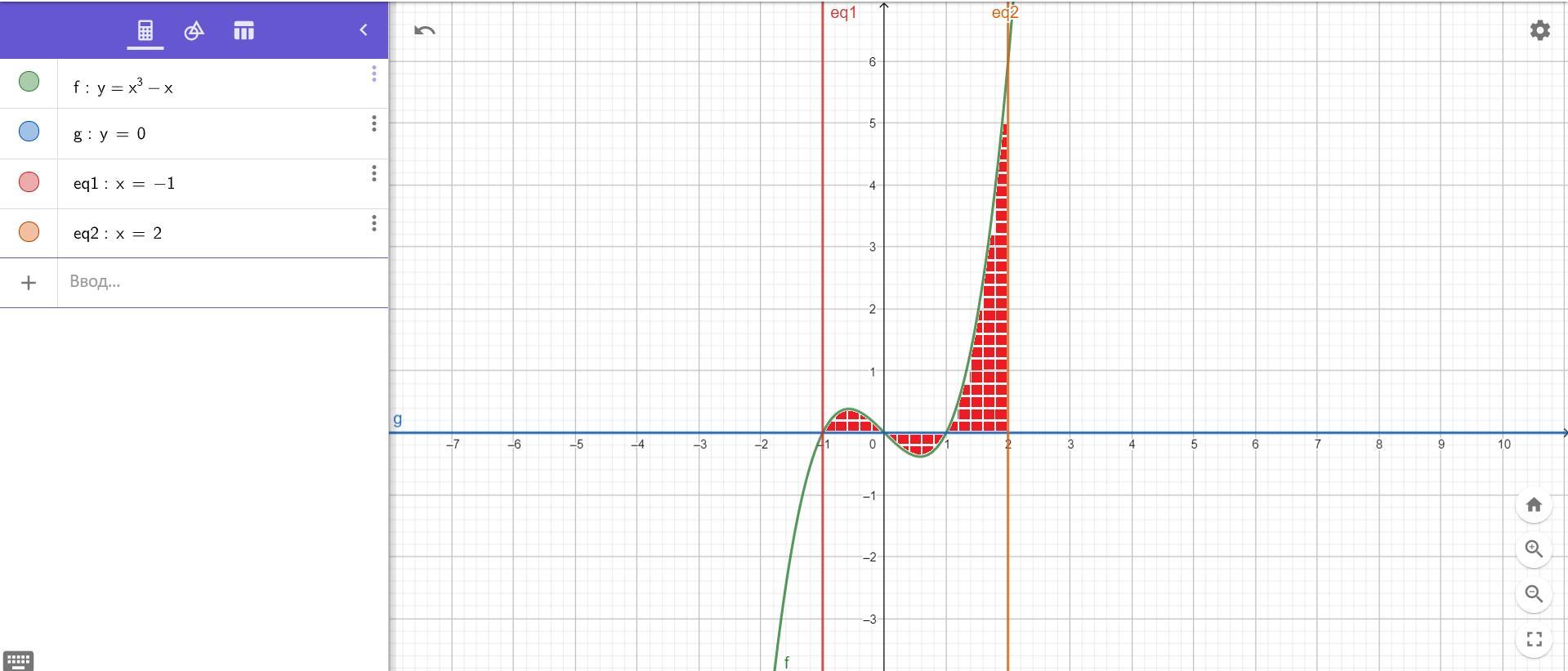
Cм. графики на фото.

Нужно найти площадь закрашеной фигуры, её можно найти как сумму площадей фигур S₁,S₂,S₃:

$S=S_1+S_2+S_3\\\\S_1=\int\limits^0_{-1} {x^3-x} \, dx\\\\S_2=-\int\limits^1_0 {x^3-x} \, dx \\\\S_3=\int\limits^2_1 {x^3-x} \, dx\\\\\\S_1=(\frac{x^4}{4}-\frac{x^2}{2})\mid^0_{-1}=\frac{0}{4}-\frac{0}{2}-(\frac{(-1)^4}{4}-\frac{(-1)^2}{2})=\frac{1}{4}\\\\S_2=-(\frac{x^4}{4}-\frac{x^2}{2}\mid^1_0)=-(\frac{1^4}{4}-\frac{1^2}{2}-(\frac{0}{4}-\frac{0}{2}))=-(-\frac{1}{4})=\frac{1}{4} \\\\ S_3=(\frac{x^4}{4}-\frac{x^2}{2})\mid^2_1=\frac{2^4}{4}-\frac{2^2}{2}-(\frac{1}{4}-\frac{1}{2})=\frac{9}{4}$

$S=S_1+S_2+S_3=\frac{1}{4}+\frac{1}{4}+\frac{9}{4}=\frac{11}{4}=2,75$