Предмет: Математика,
автор: mandzyuk2dssd
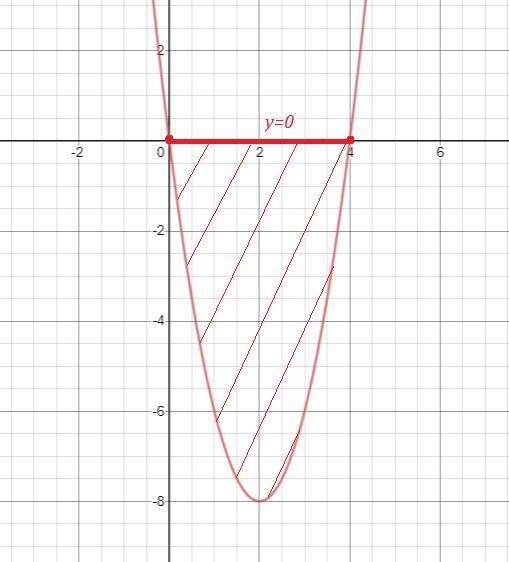
Вычислите площадь фигуры, ограниченной заданными линиями
y=2x^2-8x, y=0
Ответы
Автор ответа:
1
Ответ:
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: rohidramzes
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: olgayush81
Предмет: Алгебра,
автор: Шталь
Предмет: Химия,
автор: katarinka3