Предмет: Алгебра,
автор: issusa
Решите уравнение: (256−4^x)(x^2+2x−15)log3(x+4)=0.
Приложения:
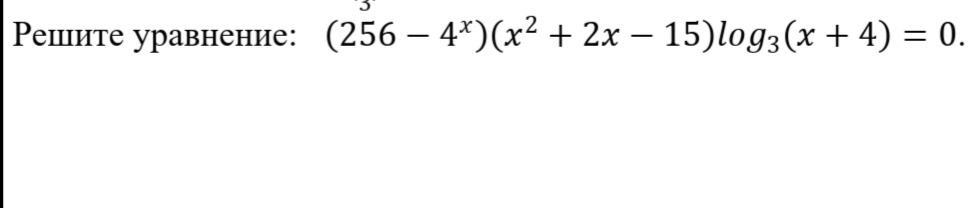
Ответы
Автор ответа:
2
.
ОДЗ: .
Произведение равно нулю когда хотя бы один из множителей равен нулю. Рассмотрим каждую скобку:
1)
2)
Отбрасываем корень из-за ОДЗ.
3)
.
Итого, корни:
Похожие вопросы
Предмет: Русский язык,
автор: narav79
Предмет: Русский язык,
автор: КотЗ
Предмет: Английский язык,
автор: dotsenkoluda
Предмет: Химия,
автор: Arela5394
Предмет: Математика,
автор: akademik005