СРОЧНОООО!!! ПЛАЧУ 40 БАЛЛОВ!!!
Ответы
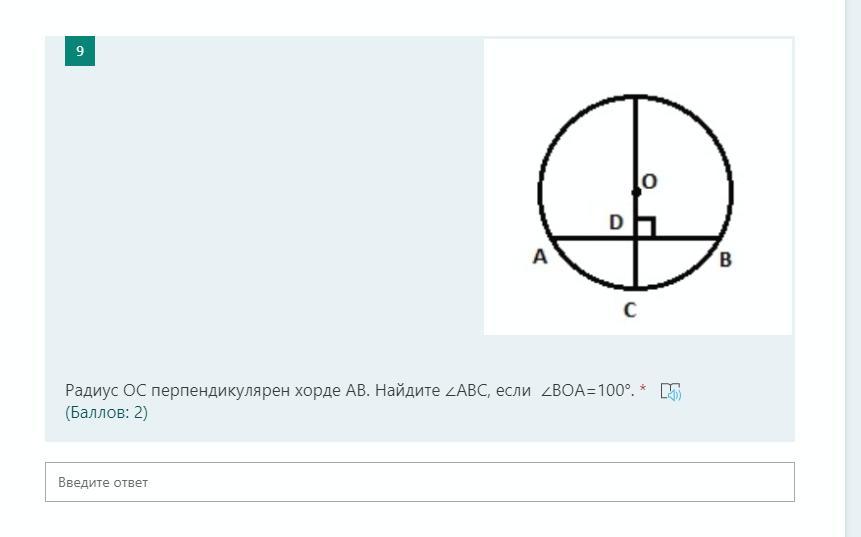
Задача#1.
Решение:
∠АОВ - центральный угол.
Центральный угол - угол, у которого вершина сам центр окружности.
Центральный угол равен дуге, на которую он опирается.
=> дуга АВ = 100°
Так диаметр КC (КO = OC) проходит через центр окружности и КC ┴ АВ => дуга АС = дуге СВ.
=> дуга АС = дуга СВ = 100°/2 = 50°
∠АВС - вписанный.
Вписанный угол - угол, у которого вершина на окружности, а стороны пересекают окружность.
Вписанный угол измеряется половиной дуги, на которую он опирается.
=> ∠АВС = 50°/2 = 25°
Ответ: 25°
Обозначьте конец диаметра точкой К. Поэтому я там писала "диаметр КС"
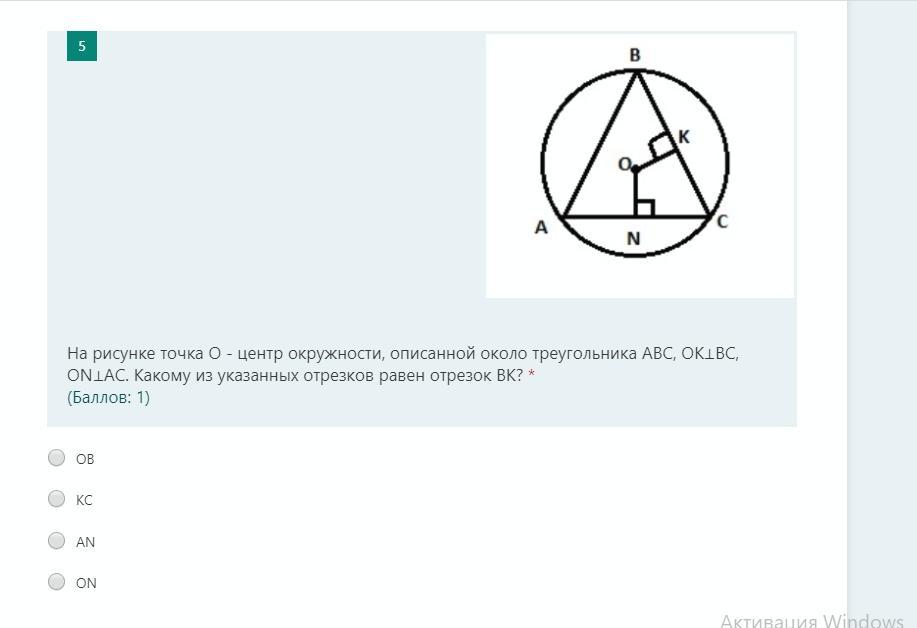
Задача#2.
Решение:
Рассмотрим △КОС и △КОВ:
Они прямоугольные, так как касательная ВС перпендикулярна к ОК, по условию.
КО - общая сторона.
ОС = ОВ, так как они радиусы окружности.
=> △КОС = △КОМ, по гипотенузе и катету.
=> ВК = КС
Ответ: КС.
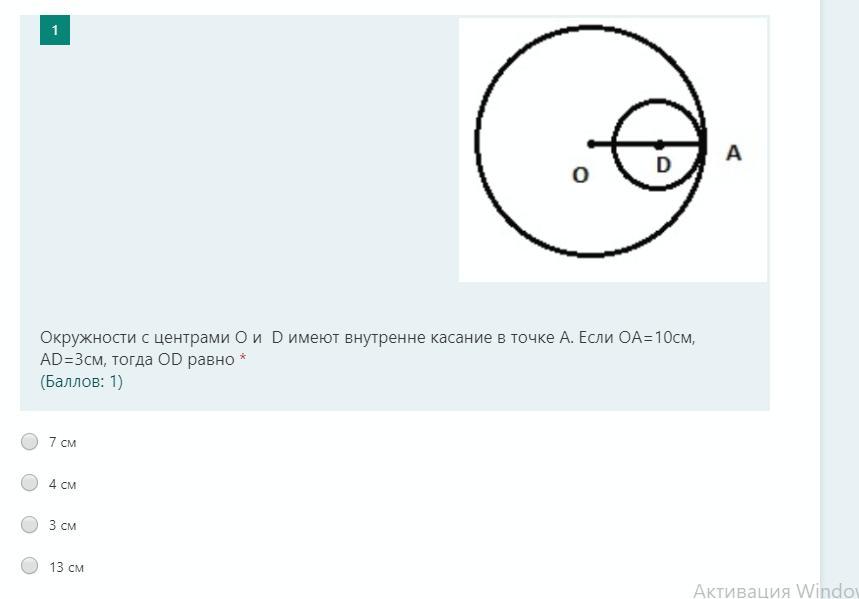
Задача#3.
Решение:
ОА = R = 10 см
AD = r = 3 см
=> OD = 10 - 3 = 7
Ответ: 7
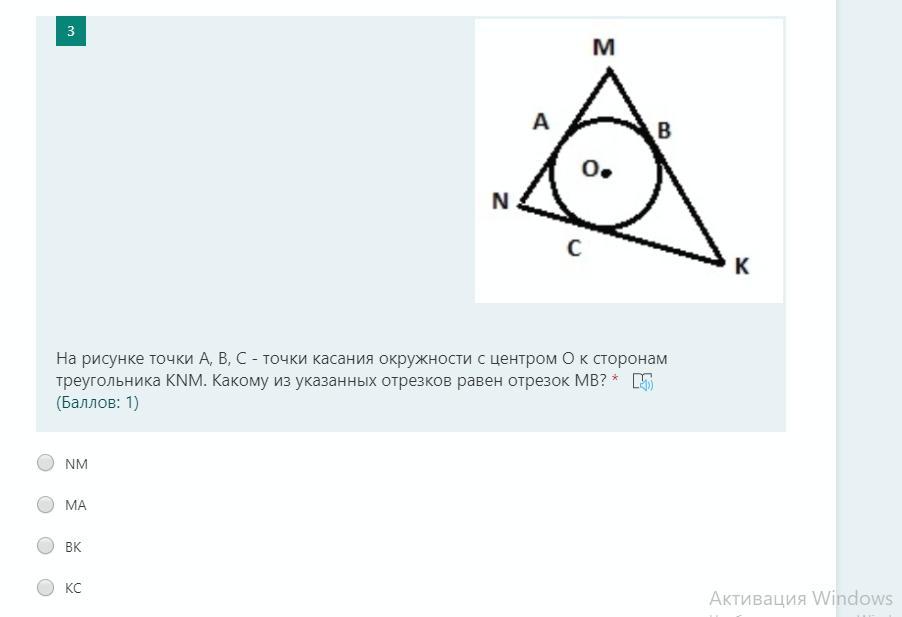
Задача#4.
Решение:
Рассмотрим △МАО и △МВО:
Они прямоугольные, так как касательные NM и МК перпендикулярны к АО и ОВ, по свойству.
АО = ОВ, так как они радиусы окружности.
ОМ - общая сторона.
=> △МАО = △МВО, по гипотенуза и катету.
=> МА = МВ
ИЛИ:
Отрезки касательных к окружности, проведённые из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
=> АМ = МВ
Ответ: МА
Задача#5
Решение:
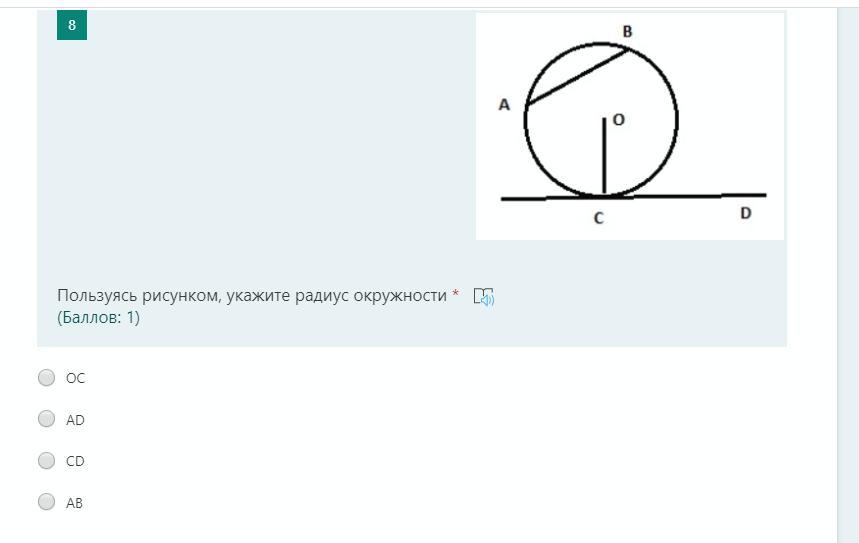
Радиус - это отрезок, соединяющий центр окружности с любой её точкой.
Хорда - отрезок, соединяющий две любые точки окружности.
=> ОС - радиус.
АВ - хорда