Предмет: Алгебра,
автор: swetlanaprya
Помогите с решением тригонометрического уравнения. Точнее, нужно проверить правильность выполнения задания (говорят, что отбор корней был неточным) . Но я не знаю, какие тут ещё корни могут быть
Приложения:

NNNLLL54:
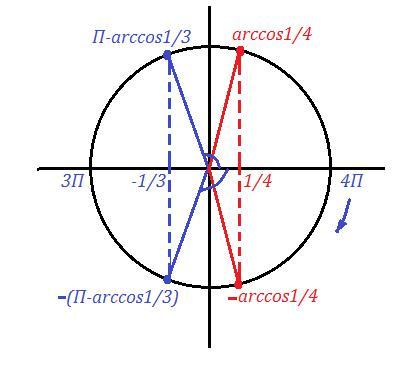
x1=4П-arccos1/4 , x2=4П-(П-arccos1/3)=3П+arccos1/3 .
А какая разница, если я использовала в х2 не 4п, а 3п?
Ой, наоборот: не 3п, а 4п?
Да блин, я ступила: первое сообщение было правильным. Прощу прощения
у вас написано: х1=4П-arccos1/3 , а надо х1=4П-(П-arccos1/3)
Ну я здесь использовала в х1: 3п+п-арккосинус 1/3. Это разве неверно?
нет, неверно нижняя точка х=(П-arccos1/3) . Чтобы получить точку из сегмента [3П;4П] ,надо от 4П в отрицательном направлении пройти к точке (П-arccos1/3), поэтому х=4П-(П-arccos1/3)=3П+arccos1/3
описка, надо: нижняя точка х=-(П-arccos1/3)
Спасибо большое, я поняла
Ответы
Автор ответа:
0
Приложения:
Похожие вопросы
Предмет: Другие предметы,
автор: rupolina
Предмет: Русский язык,
автор: klesnova
Предмет: Русский язык,
автор: vjagodka200228
Предмет: Математика,
автор: alyagromovova