Question

За даними на рисунке нужно найти S (площу) помогите пж.. Д много балов

Answer 1

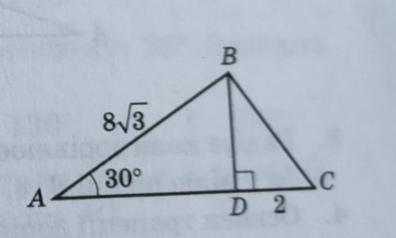
Дано: ΔABC, BD — высота на AC, AB = 8√3, DC = 2, ∠A = 30°

Найти: S ΔABC - ?

Решение:

1) Р-м ΔABD:

∠ADB = 90°  ⇒  ΔABD — прямоугольный.

Катет (BD), лежащий напротив угла (∠A) в 30°, равен половине гипотенузы (AB):

    $BD = \frac{1}{2} \cdot 8\sqrt{3} = 4\sqrt{3}$

BD = h$S\triangle = \frac{a\cdot h_a}{2} \\\\S_{ABC} = \frac{14\cdot 4\sqrt{3} }{2} = 7\cdot 4\sqrt{3} = 28\sqrt{3}$ = 4√3

2) Найдем катет AD по т. Пифагора:

    $AD=\sqrt{AB^2-BD^2} \\AD=\sqrt{(8\sqrt{3} )^2-(4\sqrt{3})^2} = \sqrt{64\cdot3 - 16\cdot 3} =\sqrt{3(64-16)} = \sqrt{3\cdot 48} = \sqrt{3\cdot 3\cdot 16} =\sqrt{9}\cdot \sqrt{16} = 3\cdot 4 = 12$

AC = a = AD+DC = 12+2 = 14

3) Подставим значения в формулу площади треугольника:

    $S_{\triangle} = \frac{a\cdot h_a}{2} \\\\S_{ABC} = \frac{14\cdot 4\sqrt{3} }{2} = 7\cdot 4\sqrt{3} = 28\sqrt{3}$

Ответ: Площадь ΔABC = 28√3 кв. ед.