Предмет: Алгебра,
автор: belarusba11
Алгебра срочно 30 балов
Приложения:
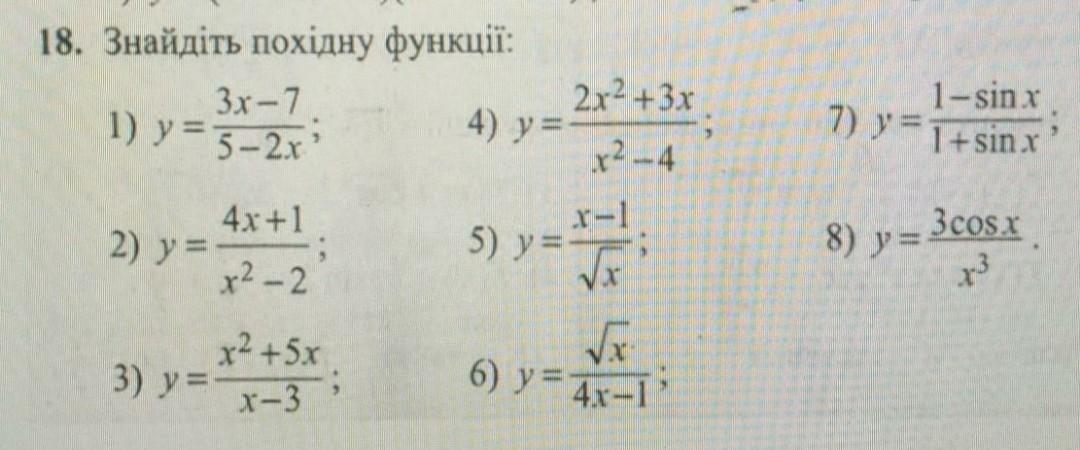
Ответы
Автор ответа:
2
belarusba11:
Спасибо, как только появится возможность выбрать лучший ответ
выберу и начисляется вам баллы
остальные
Спустя сутки такая кнопка появляется вроде бы
здравствуйте
NNNLLL54 есть задание в профиле решите пожалуйста
можеш допомогти із питанням
Похожие вопросы
Предмет: Українська мова,
автор: Катиночка
Предмет: Русский язык,
автор: Olesya2002
Предмет: Другие предметы,
автор: марина565
Предмет: Математика,
автор: kukovofiwi
Предмет: Математика,
автор: pomoshnil