Предмет: Алгебра,
автор: idel655
Найти неопределенный интеграл и результаты интегрирования проверить дифференцированием
Приложения:
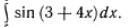
Ответы
Автор ответа:
0
Автор ответа:
0
т.к. производная аргумента равна 4, и зная, что дифференциал функции - это произведение производной на дифференциал аргумента, можно записать этот интеграл с.о. ∫sin(3+4x)dx=
∫sin(3+4x)d(3x+4)/4=-cos(3x+4)/4+c
проверка (-cos(3x+4)/4+c)'=4sin(3+4x)/4+0=sin(3+4x)
Похожие вопросы
Предмет: Русский язык,
автор: СРостова61
Предмет: Другие предметы,
автор: Весёлая888
Предмет: Английский язык,
автор: gakhmedyauova
Предмет: Литература,
автор: Nastya174002