Предмет: Геометрия,
автор: Terry23W
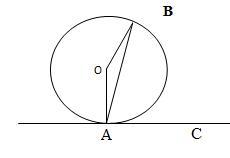
AC- касательная, AB- хорда окружности с центром в точке O, угол BAC=57 гр. Чему равен угол AOB? (см. рисунок B)
Приложения:
Ответы
Автор ответа:
1
Ответ: 114
Объяснение:
OA_I_AC по теор. о касательных, <OAC=90, <OAB=90-57=33,
тр-к OAB-ранобедр-й,, <B=33, <AOB=180-2*33=114
Terry23W:
_I_ - знак паралели?
это перпендикулярность, т.е. ⊥
благодарочка
Автор ответа:
1
Чертёж уже имеется.
- - - - - - - - - - - -
* решение * :
Радиус окружности и касательная к этой окружности пересекаются под прямым углом. Отсюда, угол ОАС = 90°.
Если угол ОАС = 90°, а угол ВАС = 57°, то угол ОАВ = 90° - 57° = 33°.
ОА = ОВ ( радиусы одной и той же окружности ) => треугольник ОАВ - равнобедренный с основанием АВ.
Углы при основании равнобедренного треугольника равны. Тогда угол ОАВ = углу ОВА = 33°.
По теореме о сумме углов в треугольнике:
угол АОВ = 180° - угол ОАВ - угол ОВА = 180° - 33° - 33° = 114°.
Ответ: 114°.
Вот и всё! :)
Похожие вопросы
Предмет: Английский язык,
автор: Джаля
Предмет: Українська література,
автор: 102798
Предмет: Русский язык,
автор: ayupova99
Предмет: Музыка,
автор: Dushina14
Предмет: Математика,
автор: настя6356