Question

Помогите пожалуйста решить

Answer 1

1) MNKP - параллелограмм. Диагонали MK и NP пересекаются и в точке пересечения, т. О, делятся пополам.Найдём координаты точки О как середины отрезка MK , а затем координаты точки Р, зная координаты т.N и координаты т.О .

$M(-2;-1)\; ,\; N(-3;1)\; ,\; K(0;1)\\\\x_{O}=\dfrac{-2+0}{2}=-1\; \; ,\; \; y_{O}=\dfrac{-1+1}{2}=0\; \; \; \to \; \; \; O(-1;0)\\\\x_{O}=\dfrac{x_{N}+x_{P}}{2}\; \; ,\; \; -1=\dfrac{-3+x_{P}}{2}\; \; ,\; \; -2=-3+x_{P}\; \; ,\; \; x_{P}=1\\\\y_{O}=\dfrac{y_{N}+y_{P}}{2}\; \; ,\; \; 0=\dfrac{1+y_{P}}{2}\; \; ,\; \; 0=1+y_{P}\; \; ,\; \; y_{P}=-1\\\\P(\, 1\, ;-1\, )$

2)  Если все стороны у четырёхугольника  равны, то этот четырёхугольник является ромбом.  Вычислим длины сторон.

$A(0;1)\; ,\; B(2;5)\; ,\; C(4;1)\; ,\; D(2;-3)\\\\AB=\sqrt{(2-0)^2+(5-1)^2}=\sqrt{4+16}=\sqrt{20}\\\\BC=\sqrt{(4-2)^2+(1-5)^2}=\sqrt{4+16}=\sqrt{20}\\\\CD=\sqrt{(2-4)^2+(-3-1)^2}=\sqrt{4+16}=\sqrt{20}\\\\AD=\sqrt{(2-0)^2+(-3-1)^2}=\sqrt{4+16}=\sqrt{20}$

Все стороны четырёхугольника равны, поэтому ABCD - ромб .

$3)\; \, (x-1)^2+(y+2)^2=9$

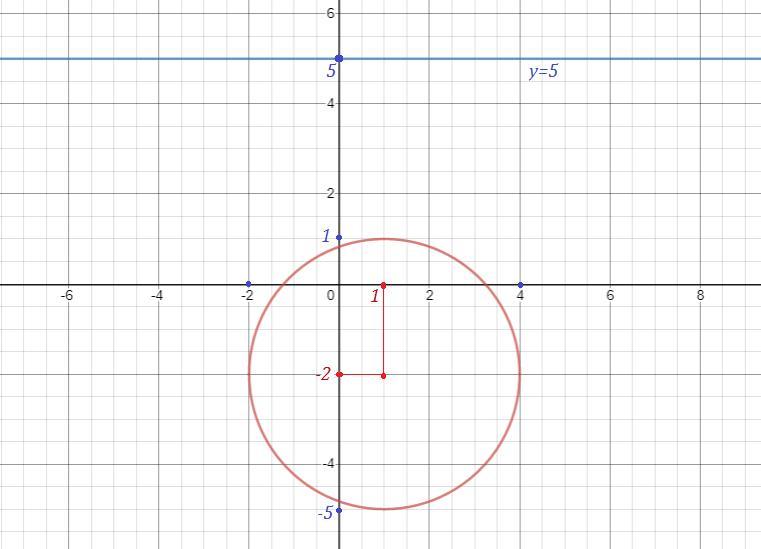
Это уравнение окружности с центром в точке С(1;-2) и радиусом R=3 .

Прямая у=5 и окружность не имеют общих точек, не пересекаются.