1. Площадь прямоугольника АВСD равна 15. Найдите сторону ВС прямоугольника, если
известно, что АВ = 5.
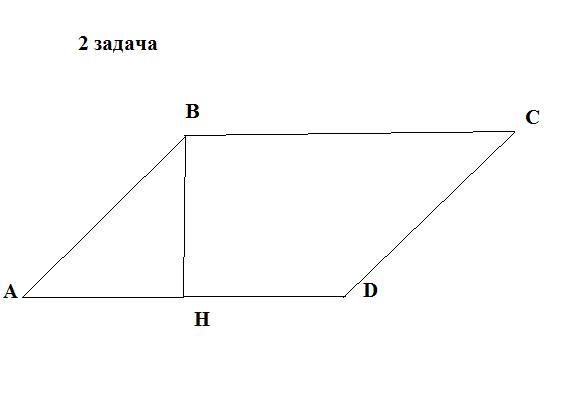
2. В параллелограмме две стороны 12 и 16 см, а один из углов 150°. Найдите площадь
параллелограмма.
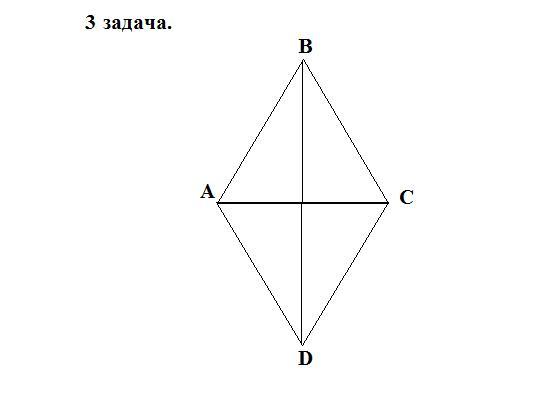
3. В ромбе АВСD проведена диагональ АС. Найдите угол АВС, если известно, что угол АСD
равен 35°.
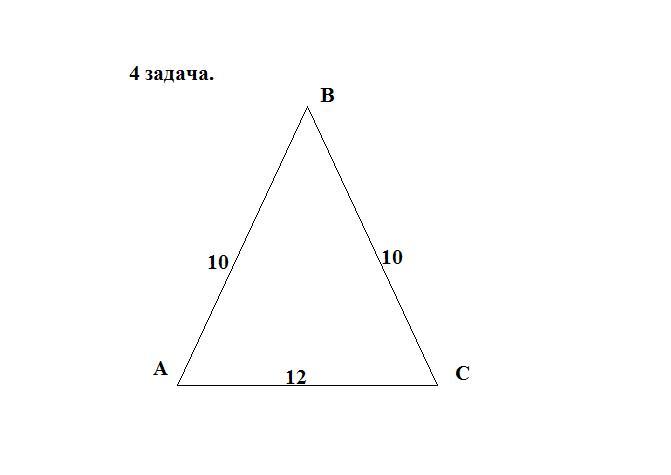
4. Найдите площадь равнобедренного треугольника со сторонами 10см, 10см и 12 см.
5. По данным рисунка найдите градусную меру
дуги Х.
120˚ 30˚ Х
6. Укажите, какие из перечисленных ниже утверждений верны:
1) Если диагонали параллелограмма равны, то он прямоугольник.
2) Если противоположные стороны четырехугольника попарно равны, то он параллелограмм.
3) Если диагонали параллелограмма перпендикулярны, то он ромб.
4) Диагонали прямоугольника являются биссектрисами его углов.
7. Сторона ромба равна 5 , а одна из его диагоналей равна 6 . Найти вторую диагональ.
8. Площадь квадрата со стороной 5
2
равна
9. Катет прямоугольного треугольника, противолежащий углу в 300
, равен 16см. Найдите
гипотенузу.
10. В прямоугольном треугольнике АВС катеты АС=3см, ВС=4см гипотенуза равна 5см. Найдите
синус угла А.
Ответы
Ответ:
1.
Пусть дан ABCD - прямоугольник, SАВСD = 15 см, АВ = 5 см.
Найдём ВС - ?
По формуле для Sпрямоуг = a×b ⇒ Sпрямоуг = AB×BC
BC=Sпрямоуг /AB
ВС=15/5 = 3 см
Ответ : ВС = 3 см
2.
Пусть дан параллелограмм ABCD,∠В= 150°, две стороны 12 и 16 см. Найдём SABCD -?
Из вершины В проведём высоту ВН к стороне АД.
∠А = 180° - ∠В = 180° - 150° = 30°.
Рассмотрим △АВН : ВН является высотой и катетом и находится против ∠30°.
АВ-гипотенуза , значит ВН = АВ : 2 = 12 : 2 = 6 см.
SABCD = ВН × АД = 6 × 16 = 96 см².
Ответ : SABCD = 96 см²
3.
Пусть дан ромб АВСD , АС- диагональ , ∠АСD = 35° .Найдём ∠АВС - ?
АС - биссектриса, ∠АСD = ∠ВАС = 35°, как накрестлежащие.
Рассмотрим △АВС : равобедренный, т.к у ромба все стороны равны, значит углы при основании равны.
∠АВС=180° - 35° - 35° = 110°
Ответ : 110°
4.
Пусть дан △АВС-равнобедренный , АС-основание = 12 см.
АВ=ВС=10 см. Найдём S△АВС-?
Рассмотрим △АВС : Проведем высоту ВН , △АВС-равнобедренный ⇒ ВН является высотой , медианой и биссектрисой. Образован прямоугольный треугольник АВН, АН = НС = 12/2 = 6 см.
По теореме Пифагора найдём катет ВН :
ВН=√АВ² - АН²
ВН=√64
ВН=8 см
S△АВС=(ВН×АС)/2
S=(8×12)/2
S=48 кв. см
Ответ:48 кв.см.
6.
2,4