Решите пожалуйста то что слева с полными развёрнутыми ответами!!! Решить на 5
Ответы
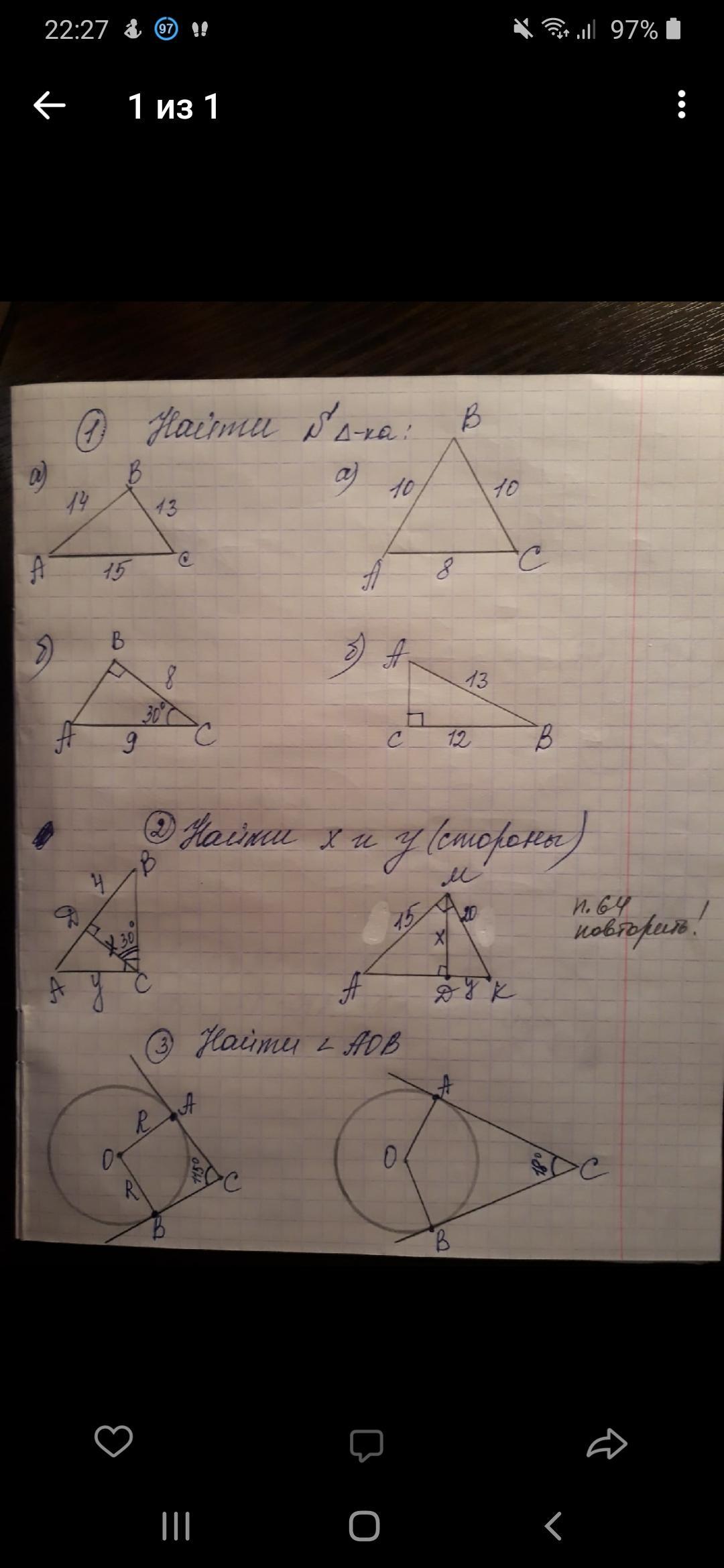
а) По теореме Герона площадь произвольного треугольника можно найти по формуле S = √p(p-a)(p-b)(p-c), где p - полупериметр треугольника, a, b, c - его стороны.
p = a+b+c/2; p = 13+14+15/2 = 21
Подставляем в формулу имеющиеся значения и вычисляем:
S = √21(21-13)(21-14)(21-15) = √21×8×7×6 = √7×3×2×4×7×2×3 (раскладываем числа на множители, чтобы было проще выделить корень) = √7^2+3^2+2^2+2^2 = 7×3×2×2 = 84.
Ответ: 84.
б) Площадь треугольника можно найти по формуле S = 1/2ab×sinu, где a, b - соседние стороны, sinu - синус угла между этими сторонами. Подставляем в формулу данные значения и вычисляем:
S = 1/2×8×9×sin30 = 1/2×8×9×1/2 = 18.
Ответ: 18.
в) В прямоугольном треугольнике катет, лежащий против угла в 30°, равен половине гипотенузы. Значит, в прямугольном треугольнике DBC гипотенуза BC = 2DB; BC = 2×4 = 8. По теореме Пифагора DB^2+DC^2 = BC^2. Выражаем отсюда неизвестную сторону.
DC = √BC^2-DB^2; DC = √64-16 = √48 = 4√3.
В прямоугольном треугольнике ADC угол DCA = 90-30 = 60°, значит угол A = 180-90-60 = 30°. Катет DC, лежащий против угла A = 30°, равен половине гипотенузы AC. Следовательно, AC = 2DC, AC = 2×4√3 = 8√3.
Ответ: x = 4√3, y = 8√3.
г) Проведём отрезок ОС. Треугольники ОАС и ОВС - прямоугольные, т.к. касательные к окружности перпендикулярны радиусам ОА и ОВ, проведенным в точки касания. Значит, углы ОАС и ОВС равны 90°. ОАСВ - четырёхугольник, сумма всех его углов равна 360°. Следовательно, угол АОВ = 360-90-90-115 = 65°.
Ответ: 65°.