cos(a+b)+cos(a-b)---------------------sin(a+b)+sin(a-b)
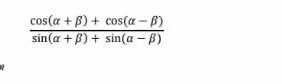
Ответы
Упростить ( cos(α+β) +cos(α -β) ) / ( sin(α+β) + sin(α -β) )
- - - - - - -
cos(α+β) =cosα*cosβ - sinα*sinβ и cos(α- β) =cosα*cosβ +sinα*sinβ ⇒
cos(α+β) + cos(α- β) =2 cosα*cosβ (1)
sin(α+β) =sinα*cosβ + cosα*sinβ и sin(α- β) =sinα*cosβ - cosα*sinβ ⇒
sin(α+β) + sin(α - β) = 2sinα*cosβ (2)
Из (1) и (2) получаем ( cos(α+β) +cos(α -β) ) / ( sin(α+β) +sin(α -β) ) =
2 cosα*cosβ /2sinα*cosβ =ctgα
2 -ой способ || применение формул преобразование сумм тригонометрических функций в произведения :
* * * cosA + cosB=2cos(A + B)/2 *cos(A -B)/2 * * *
* * * sinA + sinB =2sin(A + B)/2 *cos(A - B)/2 * * *
* * * A =α + β ; B = α - β * * *
- - - - - - - -
( cos(α+β) +cos(α -β) ) / ( sin(α+β) +sin(α -β) ) = 2cosα*cosβ / 2sinα*cosβ = ctgα