Предмет: Математика,
автор: Onmyway1
пожалуйста помогите решить это неравенство, очень нужно
Приложения:
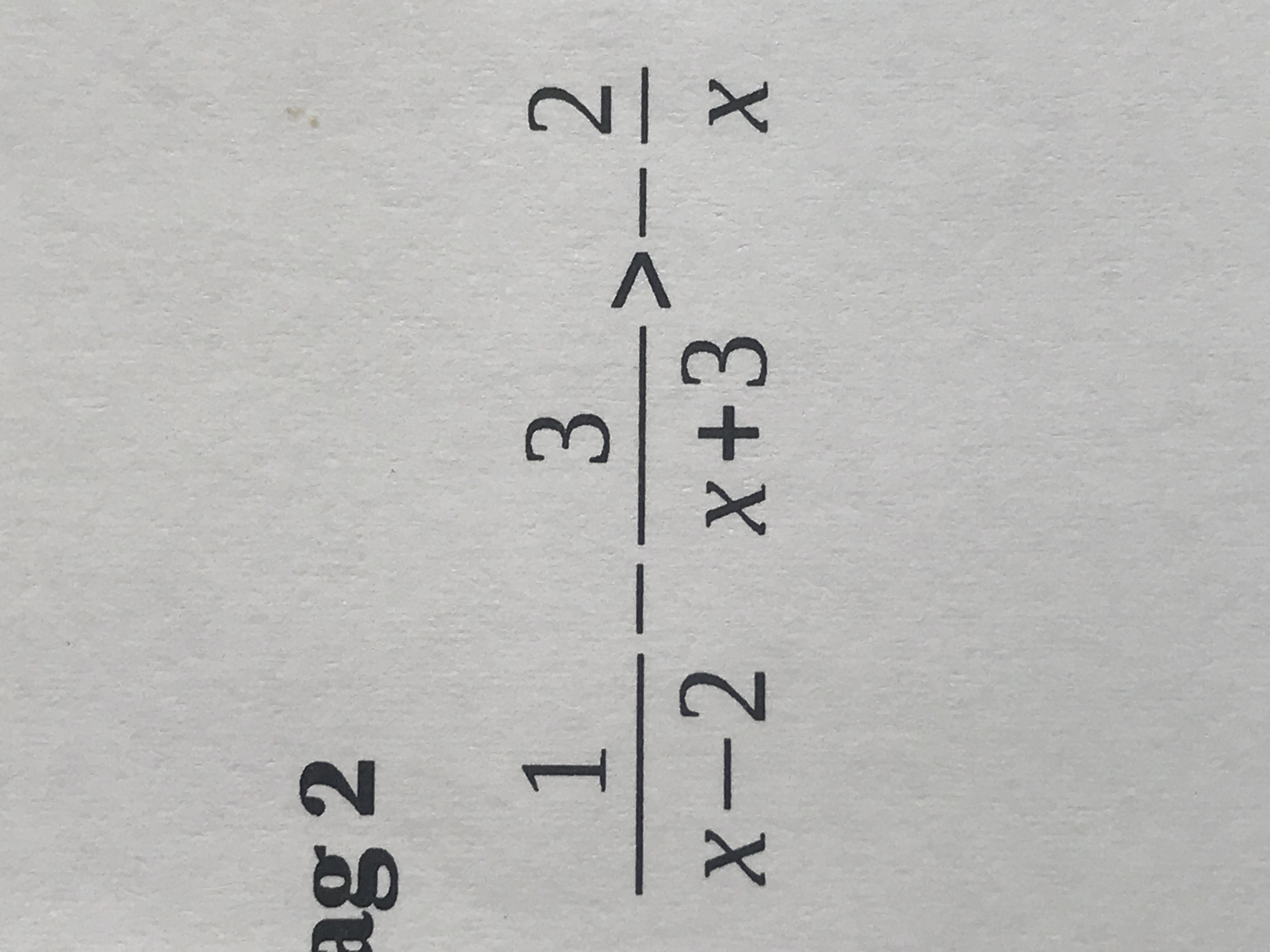
Ответы
Автор ответа:
1
Ответ: x∈ (-∞, -3) ∪ (0, 12/11) ∪(2, +∞)
Пошаговое объяснение:
-
> -2/x, x≠2, x≠ -3, x≠0
1/x-2 -3/x+3 +2/x >0
>0
>0
>0
>0
>0
Ответ: x∈ (-∞, -3) ∪ (0, 12/11) ∪(2, +∞)
Похожие вопросы
Предмет: Русский язык,
автор: indira05com123
Предмет: Русский язык,
автор: СВЕТА1233214
Предмет: Українська мова,
автор: 0995634837
Предмет: Физика,
автор: hilkou
Предмет: Литература,
автор: оля1431