Предмет: Математика,
автор: Karluginvlad
Найти производные функций
Приложения:
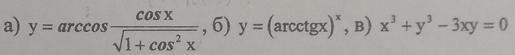
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: dimas152003
Предмет: Русский язык,
автор: yakotoeya
Предмет: Геометрия,
автор: Dredison