Предмет: Геометрия,
автор: xxxxxxxx222
Найти: АС помогите с решением
Приложения:
Ответы
Автор ответа:
5
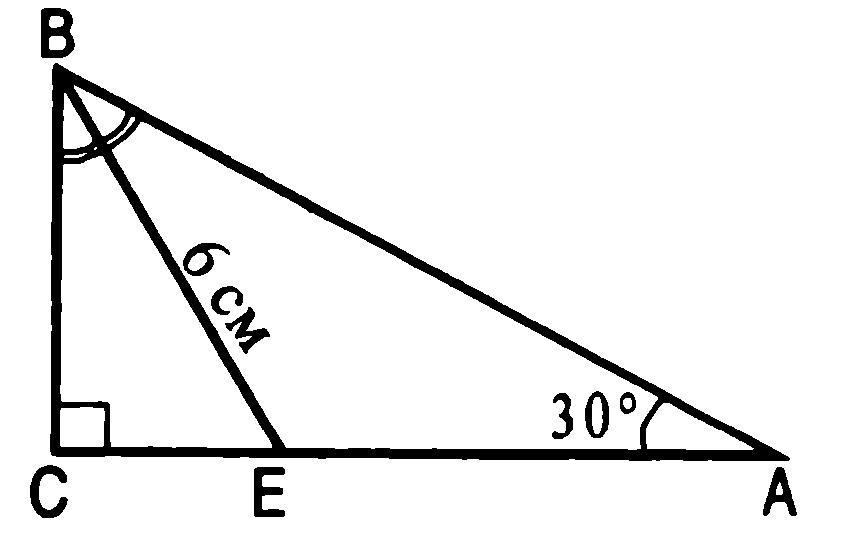
Дано:
△ABC - прямоугольный.
△BEA - тупоугольный.
BE - 6 см. (биссектриса)
∠A = 30˚.
∠C = 90˚.
Найти:
AC.
Решение.
СУММА ОСТРЫХ УГЛОВ В ПРЯМОУГОЛЬНОМ ТРЕУГОЛЬНИКЕ РАВНЯЕТСЯ 90°.
=> ∠B = 90 - 30 = 60˚.
Т.к. BE - биссектриса => ∠EBA = ∠CBE = 60 : 2 = 30˚
=> △EBA - равнобедренный (т.к. ∠A = ∠EBA = 30˚)
СУММА ОСТРЫХ УГЛОВ В ПРЯМОУГОЛЬНОМ ТРЕУГОЛЬНИКЕ РАВНЯЕТСЯ 90°.
=> ∠CBE = 90 - 30 = 60˚.
Если острый угол в прямоугольном треугольнике равняется 30°, то напротив лежащий катет равен половине гипотенузы.
=> CE = 3 см.
Т.к. △EBA - равнобедренный => BE = EA = 6 см.
=> AC = 6 + 3 = 9 см.
Ответ: 9 см.
Похожие вопросы
Предмет: Другие предметы,
автор: башенка
Предмет: Английский язык,
автор: aiida98
Предмет: Русский язык,
автор: Мила01Бога
Предмет: Математика,
автор: Andreyryl
Предмет: Математика,
автор: arefevayulya