Помогите решить задачу

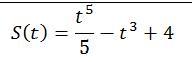
Ответы
Ответ:
Объяснение: a(t)=v'(t)
v(t)=s'(t)
v(t)=s'(t)=(t⁵/5-t³ +4)'=1/5·5t⁴-3t²=t⁴-3t²
a(t)=v'(t)=(t⁴-3t²)'=4t³-6t
a(t)=2, 4t³-6t=2
4t³-6t-2=0 Надо решить кубическое уравнение. Определим делители свободного члена: ±1;±2. Методом подбора найдем один корень
4·(-1)³-6·(-1)-2=-4+6-2=0, t=-1 - первый корень, (t+1) - первый множитель в разложении тричлена на множители. Разделим тричлен на (t+1) в столбик:
4t³ +0·t² - 6t - 2 ║t+1
4t³ +4t² 4t²-4t-2
-4t² - 6t
-4t² - 4t
-2t - 2
-2t - 2
Найдем корни 4t²-4t-2=0, D=16-4·4·(-2)=48
t₁=(4-√48)/8=(1-√3)/2 меньше 0, t₂=(4+√48)/8=(1+√3)/2
Тричлен раскладывается на множители
4t³-6t-2=(t+1)(t-(1-√3)/2)(t-(1+√3)/2)
Нас интересуют только положительные ответы, т.е. только t=(1+√3)/2