Предмет: Геометрия,
автор: nauka
В правильной четыреугольной пирамиде высота равна 5, боковое ребро =13 найти объем пирамиды
Ответы
Автор ответа:
0
Найдём половину диагонали основы из теоремы Пифагора:
Сторона квадрата равна диагонали деленое на :
Объем:
Автор ответа:
0
Решение указано ниже на фотографии
Ответ: 480 см в кубе
Приложения:
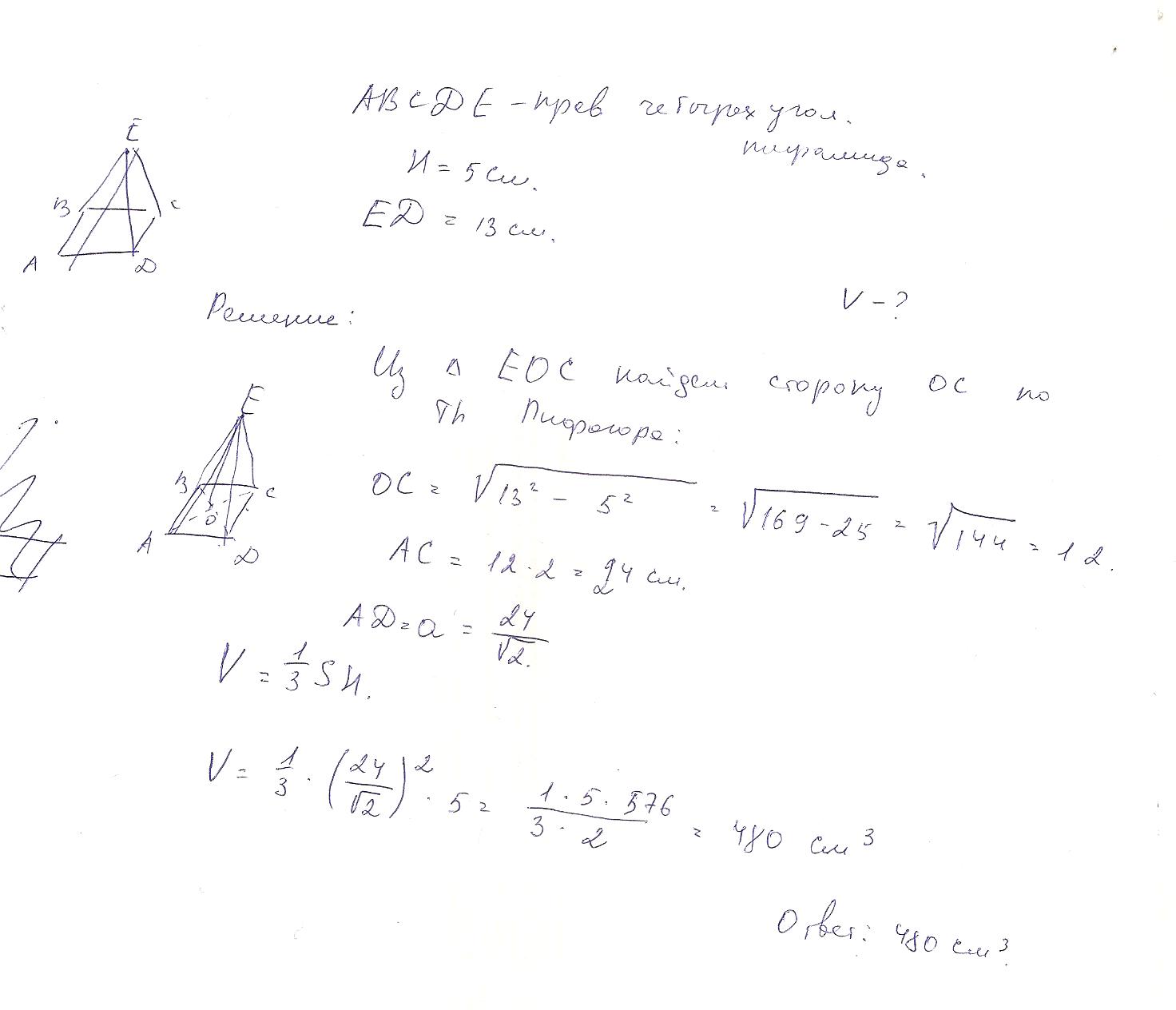
Похожие вопросы
Предмет: Химия,
автор: artemiskaplun1
Предмет: Математика,
автор: Dora132
Предмет: Литература,
автор: gzubs927
Предмет: Математика,
автор: oktavia