Предмет: Математика,
автор: li4ka2011
Найти интеграл функции
Приложения:
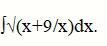
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Другие предметы,
автор: potapoffsasha
Предмет: Русский язык,
автор: н2а0н1а3
Предмет: Английский язык,
автор: москаленковна
Предмет: Математика,
автор: kostrominataty