Предмет: Алгебра,
автор: flexadile
Решить неравенство:
Приложения:
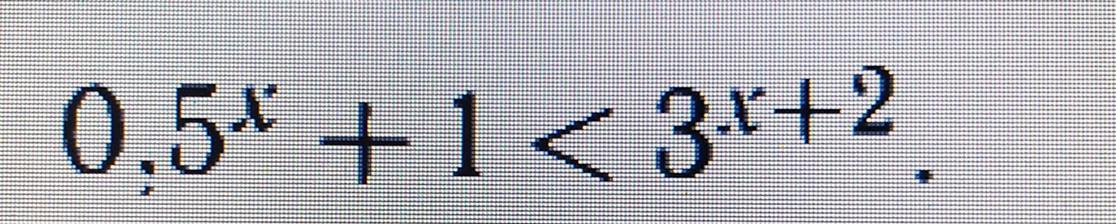
Ответы
Автор ответа:
1
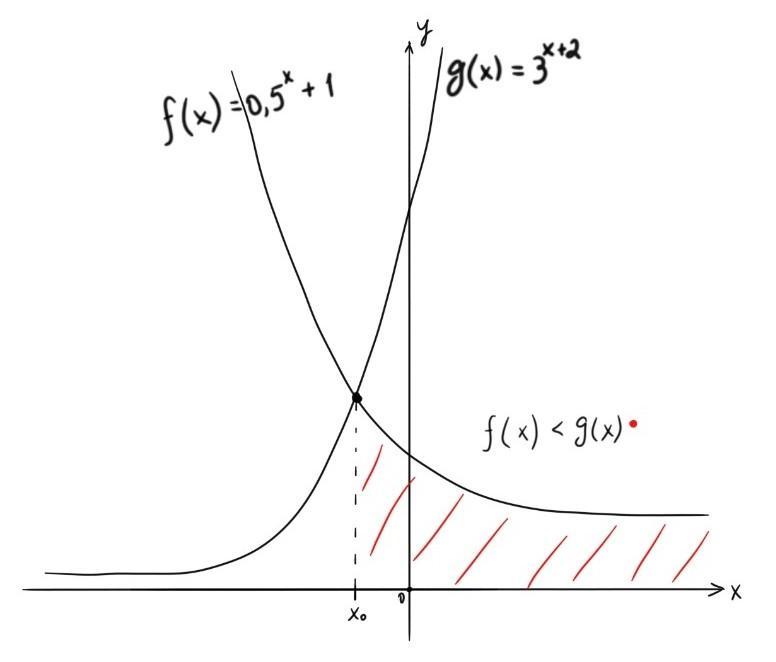
Более альтернативного решения не видно, поэтому применяем подбор предварительно начертив приблизительный график обеих функций.
На графике видно, что пересечение функций одно (корень х₀) и решением будет все числа по правой части от корня. Осталось найти корень, но данное неравенство не решить обычными методами, поэтому пробуем подбор:
Корень найден, хоть и не самым лучшим методом. Можно писать ответ:
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Valik898989
Предмет: Английский язык,
автор: 8842040
Предмет: Русский язык,
автор: 102030555n
Предмет: Математика,
автор: ксюша1373
Предмет: Алгебра,
автор: Bozhena127