Предмет: Геометрия,
автор: skyguardian04
сторона правильного шестиугольника вписанного в окружность равна 7 см. найдите периметр правильного треугольника вписанного в эту окружность
Ответы
Автор ответа:
78
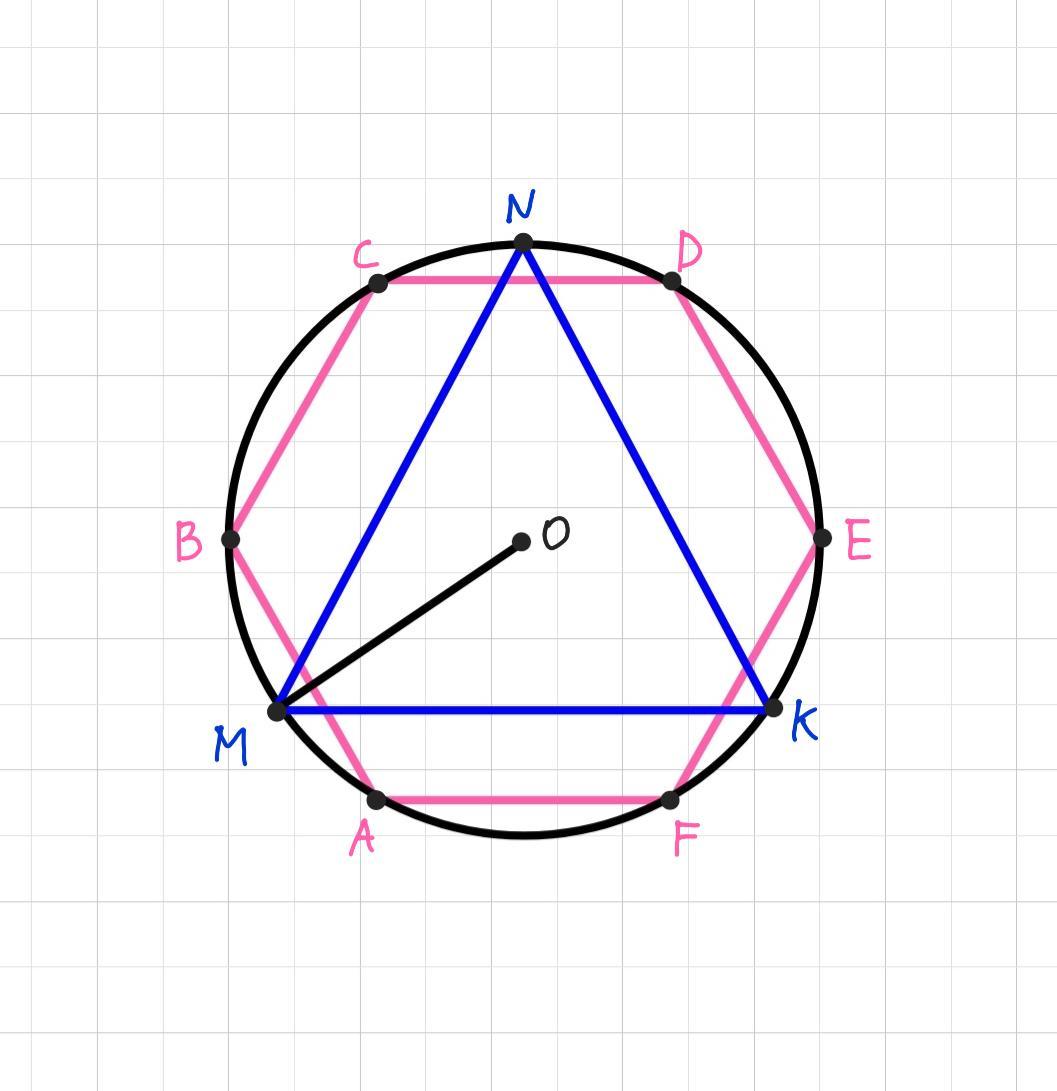
Дано: окружность, т.О - центр, ABCDEF - впис. прав. 6-угольник, АВ= 7 см, MNK - впис. прав. треугольник.
Найти: Рmnk.
Решение.
1) Радиус описанной окружности всегда равен стороне правильного шестиугольника, поэтому сразу делаем вывод, что радиус данной окружности равен стороне данного правильного шестиугольника. R=AB= 7 см.
2) Радиус описанной окружности правильного треугольника, выраженный через его сторону, равен:
R= √3/3 • а, где R - радиус, а "а" - сторона прав. треугольника.
Находим сторону треугольника ΔMNK.
7= √3/3 • MN;
MN= 7: √3/3;
MN= 7• 3/√3;
MN= 21/√3= 21√3/3= 7√3 (см)
3) Периметр треугольника MNK
Pmnk= 3MN= 3•7√3= 21√3 (см)
Ответ: 21√3 см.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: ivanovskayajen
Предмет: Английский язык,
автор: Альберт2013
Предмет: Русский язык,
автор: Кристюшка558
Предмет: Химия,
автор: kot3TToDHaPkOtE